Переходные процессы в электрических цепях

Переходный процесс в электрической цепи – это квазистационарный процесс установления нового режима в электрической цепи, возникающий в момент ее коммутации. Коммутацией называют любые скачкообразные переключения пассивных элементов цепи или источников энергии. Переходный процесс является промежуточным между прежним, установившимся процессом, существовавшим до коммутации, и новым, устанавливающимся в цепи. Значения токов и напряжений становятся близкими к установившимся практически через конечные промежутки времени. Физическая причина переходных процессов – перераспределение энергии в реактивных элементах цепи (катушках индуктивности и конденсаторах), происходящее вследствие коммутации.

Время, после которого можно считать переходные процессы оконченными, зависит от параметров L, C, R и от требований к точности рассмотрения процессов. В электрических цепях длительность переходных процессов составляет малые доли секунды. Поэтому наличием переходных процессов во многих случаях можно пренебречь.

Переходные процессы, происходящие в цепях под воздействием импульсных напряжений и токов, имеют очень большое значение. Импульсы, используемые в радиолокации, обладают длительностью от нескольких сотен до десятых долей микросекунды, поэтому длительность переходных процессов становится соизмеримой с длительностью самих импульсов.

Рассмотрим переходные процессы в цепях с индуктивностью и емкостью.

Существует несколько методов анализа линейных цепей. Мы воспользуемся классическим методом, который основан на решении системы интегродифференциальных уравнений для исследуемой цепи; полученную систему уравнений сводят в общем случае к линейному неоднородному уравнению n-го порядка, где n определяется числом реактивных элементов цепи.

1. Переходные процессы в цепях с индуктивностью

В цепях с большой индуктивностью при резком изменении тока в результате размыкания или замыкания цепи ярко выражено явление самоиндукции. По правилу Ленца дополнительные токи, возникающие в проводниках вследствие самоиндукции, всегда направлены так, чтобы препятствовать изменению тока, текущего в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при ее размыкании происходит не мгновенно, а постепенно.

Найдем характер изменения тока при размыкании цепи. Перед отключением источника тока (при 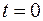) в катушке течет ток 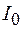. При размыкании ключа К в цепи, состоящей из катушки и лампочки (рис. 106.1), начинает действовать . Так как ток за малое время уменьшается на значительную величину, то 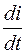– велико и тогда может оказаться, что 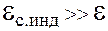. Поэтому лампочка, перед тем как погаснуть, ярко вспыхивает. 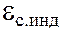создает в цепи ток того же направления, что и ток, созданный источником. Поэтому уменьшение тока при размыкании происходит постепенно.

Установим закон убывания тока с течением времени после отключения источника тока. По закону Ома, мгновенное значение силы тока 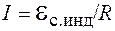, где R – сопротивление катушки и лампочки. С учетом формулы (88.3) получаем:

,

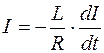откуда

.

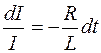Интегрируя, находим:

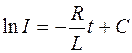. (106.1)

Учитывая, что при 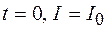, из выражения (106.1) имеем

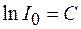. (106.2)

Из формул (106.1) и (106.2) получаем:

.

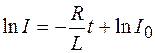После потенцирования находим:

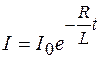. (106.3)

Из выражения (106.3) видно, что уменьшение тока в цепи происходит тем медленнее, чем больше индуктивность и чем меньше сопротивление цепи. При 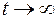, 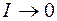. Скорость установления тока в цепи характеризуется постоянной времени цепи 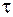(временем релаксации). Так называют время, в течение которого ток в цепи изменяется от своего установившегося значения в е раз.

Таким образом, по определению при 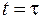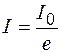(рис.106.2). Тогда из формулы (106.3) получаем:

.

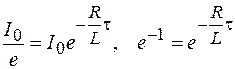Отсюда следует

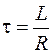. (106.4)

Формула (106.4) показывает, что время релаксации определяется свойствами самой цепи. Скорость установления тока в цепи тем больше, чем меньше индуктивность L и чем больше сопротивление R. Время установления тока в цепи можно приближенно принять равным величине t. Учитывая явление самоиндукции, не следует резко размыкать цепь, содержащую индуктивность. Возникшая при этом 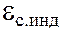может привести к пробою изоляции и порче приборов. В случае наличия в цепи большой индуктивности необходимо перед ее размыканием плавно уменьшить силу тока до безопасного значения.

Получим теперь закон изменения силы тока в цепи при подключении источника ЭДС. Нарастание тока приводит к появлению ЭДС самоиндукции и по закону Ома следует: 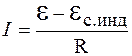. Подставив выражение для ЭДС самоиндукции, получим:

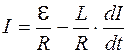. (106.5)

Поскольку в установившемся режиме 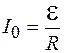, то соотношение (106.5) можно преобразовать к виду

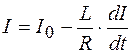
или

.

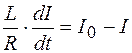Произведем замену переменной, обозначив 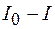через 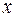. Тогда 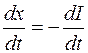и формула (106.5) преобразуется к виду, удобному для интегрирования:

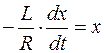
или

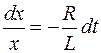. (106.6)

Теперь интегрируем выражение (106.6):

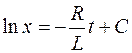
и подставляем :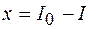

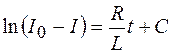. (106.7)

Постоянную интегрирования С определим из начальных условий: при 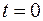, , 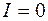т. е. и выражение (106.7) принимает вид

.

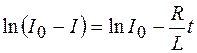Теперь выполним потенцирование:

и получим выражение для силы тока в момент времени t после подключения источника ЭДС:

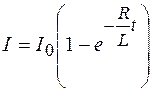. (106.8)

График этой зависимости представлен на рисунке 106.3.

Таким образом, наличие индуктивности в цепи обусловливает плавное изменение в ней силы тока при подключении и отключении источника ЭДС, т. е. сила тока в цепи с индуктивностью не может меняться скачком.

2. Переходные процессы в цепи, содержащей активное сопротивление и емкость

Рассмотрим R-С-контур (рис. 106.4). Если переключатель П поставлен в положение 1, то происходит зарядка конденсатора и по цепи течет ток зарядки 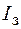. По правилу Кирхгофа для замкнутого контура в этом случае

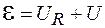, (106.9)

,

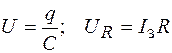где 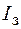и q – мгновенные значения тока зарядки и заряда на обкладках конденсатора.

Так как , а , то соотношение (106.9) преобразуем к виду

, (106.10)

где U – напряжение на обкладках конденсатора.

Разделив все члены равенства (106.10) на величину СR, имеем

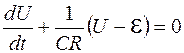. (106.11)

Обозначим

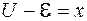. (106.12)

Продифференцируем это выражение по времени, учитывая при этом, что :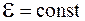

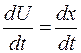. (106.13)

Выражения (106.12) и (106.13) подставим в формулу (106.11):

,

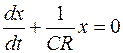или

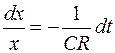. (106.14)

Решая дифференциальное уравнение (106.14), находим 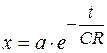или 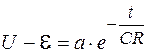. Отсюда получаем:

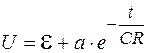. (106.15)

Константуа в уравнении (106.15) найдем из начальных условий: при 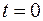, 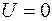. Следовательно,

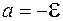. (106.16)

Объединяя выражения (106.15) и (106.16), получим для напряжения при зарядке конденсатора:

.

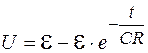Отсюда находим:

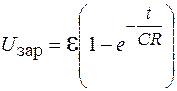. (106.17)

Выражение (106.17) показывает, что напряжение на обкладках конденсатора при его зарядке возрастает по экспоненциальному закону от нуля до ЭДС источника (рис. 106.5). По такому же закону меняется и заряд на обкладках конденсатора.

Пусть теперь переключатель П в схеме, изображенной на рисунке 106.4, переводится в положении 2. Тогда начнется разрядка конденсатора через резистор и по цепи потечет ток разрядки 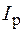, направление которого противоположно току зарядки. Поэтому

.

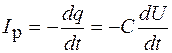Напряжение на резисторе или

.

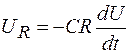В любой момент времени напряжение на конденсаторе и резисторе одинаково. Поэтому .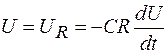

Отсюда получаем: .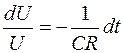

Решая это дифференциальное уравнение, находим:

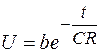. (106.18)

В начальный момент времени при 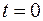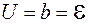. Тогда выражение (106.18) принимает вид

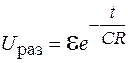. (106.19)

Из формулы (106.19) следует, что при разрядке конденсатора напряжение на обкладках убывает от ЭДС источника по экспоненциальному закону до нуля (рис. 106.6). Формулы (106.17) и (106.19) показывают, что процессы зарядки и разрядки конденсатора происходят не мгновенно, а с конечной быстротой. Скорость изменения напряжения на обкладках конденсатора определяется временем релаксации 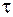, за которое напряжение на обкладках конденсатора уменьшается в е раз. Тогда при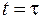 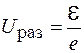. При этом из формулы (106.19) находим:

.

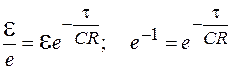Отсюда

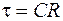. (106.20)

Таким образом, в R-С-контуре протекают апериодические процессы зарядки и разрядки конденсатора соответственно при подключении и отключении источника ЭДС. Процессу можно придать периодический характер, если периодически пополнять энергию конденсатора от источника ЭДС. Роль переключателя может выполнять газоразрядный диод. Это используется в генераторе релаксационных колебаний.