Работа и мощность в цепи квазистационарного тока

Пусть цепь квазистационарного тока содержит только активное сопротивление, напряжение на котором определяется выражени- ем (108.2). В такой цепи ток и напряжение совпадают по фазе. Поэтому ток в резисторе изменяется в соответствии с выражением (108.4).

В течение малого промежутка времени переменный ток можно рассматривать как постоянный, и поэтому мгновенная мощность переменного тока равна произведению мгновенных значений тока и напряжения:

.

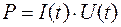Подставляя формулы для тока и напряжения, получаем:

. (109.1)

Обычно находят среднее за период значение мощности 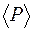. Как видно из формулы (109.1), 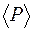определится средним за период значением квадрата синуса. Так как 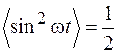, то находим:

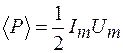. (109.2)

Выражение (109.2) можно записать в виде

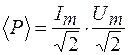. (109.3)

Величины

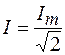и 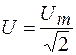(109.4)

называют действующими (эффективными) значениями силы тока и напряжения. Тогда формула (109.3) принимает вид

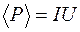. (109.5)

Выражение (109.5) совпадает с формулой мощности постоянного тока. Поэтому действующие значения переменного тока и напряжения можно приравнять к значениям постоянного тока и напряжения, при которых в цепи выделяется такая же мощность, как и при переменном токе. Амперметры и вольтметры, включенные в цепь переменного тока, измеряют действующие значения тока и напряжения.

Если же цепь содержит не только активное, но и реактивное сопротивления, то между током и напряжением в цепи возникает сдвиг фаз на некоторую величину j. При этом напряжение в цепи можно разложить на две составляющие: активную 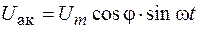, колеблющуюся в фазе с током, и реактивную 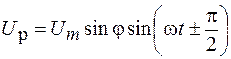, смещенную по фазе относительно тока на 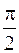. Соответственно этому при вычислении работы за период Т получим тоже два слагаемых. Одно из них, обусловленное реактивной составляющей напряжения, равно нулю, так как реактивное сопротивление не потребляет энергии. Следовательно, полная работа за период определяется только активной составляющей напряжения. Тогда

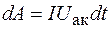. (109.6)

Учитывая, что 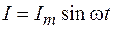и 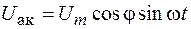, из соотношения (109.6) получаем 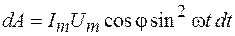. Работа за период

.

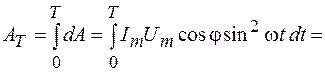
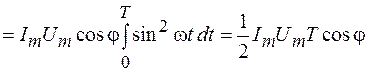Поэтому средняя мощность 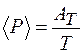, или

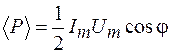. (109.7)

Введя в выражение (109.7) действующие значения тока и напряжения, находим:

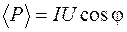. (109.8)

Сравнивая равенства (109.5) и (109.8), видим, что они отличаются наличием дополнительного множителя 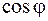, который называют коэффициентом мощности цепи. Формула (109.8) показывает, что в общем случае выделяемая в цепи квазистационарного тока мощность зависит не только от силы тока и напряжения, но еще и от сдвига фаз между током и напряжением. При сдвиге фаз между током и напряжением 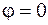формула мощности (109.8) имеет такой же вид, как и для цепей постоянного тока. Такой режим называется согласованным, мощность полностью поглощается нагрузкой. При 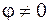часть мощности "отражается" обратно к источнику.