Получение переменного тока

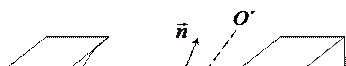Рассмотрим вращение замкнутого контура (рамки) в однородном магнитном поле с индукцией 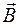(рис. 107.1). Пусть в начальный момент времени ( 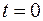) рамка расположена так, что 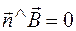. Рамка вращается равномерно с угловой скоростью 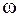относительно оси OO'. К моменту времени t рамка повернется на угол

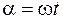. (107.1)

Тогда поток вектора 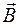через рамку в любой момент времени t будет равен

. (107.2)

Из формулы (107.2) следует, что поток Ф через рамку с течением времени будет меняться. На основании закона Фарадея в рамке при этом возникает ЭДС индукции:

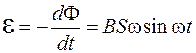. (107.3)

Как видно из соотношения (107.3), возникающая в контуре ЭДС меняется периодически с течением времени. Если R – сопротивление провода, из которого изготовлена рамка, то сила тока в рамке

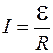. (107.4)

Объединяя выражения (107.3) и (107.4), находим:

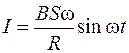. (107.5)

Из равенства (107.5) следует, что ток в рамке с течением времени меняется периодически, т. е. является переменным.

В формуле (107.3) величина

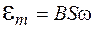(107.6)

является амплитудой ЭДС. Тогда это выражение можно записать в виде

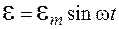. (107.7)

В соотношении (107.5) величина 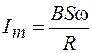является амплитудой силы тока, тогда .

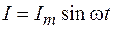На основании формул (107.7) и (107.5) заключаем, что графики зависимосте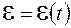й и 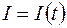имеют вид, изображенный на рисунке 107.2. Сила тока и ЭДС одновременно обращаются в нуль и одновременно достигают максимальных значений.

Анализ формулы (107.6) показывает, что 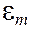существенно зависит от индукции магнитного поля 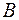(возрастает с увеличением магнитной проницаемости) и от числа витков рамки (увеличивается 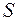). Вращение рамки в магнитном поле объясняет принцип действия генераторов электрического тока.