Анализ цепей переменного тока.

2.1. Переменные тока. напряжения. ЭДС. Основные понятия. определения.

Переменные ток, напряжение , ЭДС -это такие ток , напряжение, ЭДС , которые изменяются во времени по периодическим законам. Встречаются периодические и непериодические токи, напряжения и ЭДС. Наибольшее распространение имеют периодические напряжения.

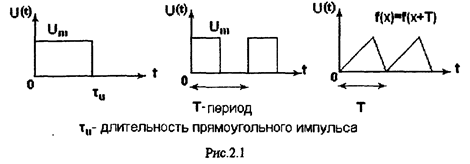
Гармонические токи и напряжения.

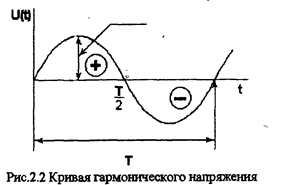
Гармонические токи, и напряжения - это такие токи и напряжения, которые изменяются во времени по гармоническим законам (см. рис.2.2)

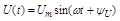
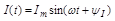
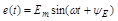
где и(ft), i(t), e(t) - мгновенные значения напряжения, тока и ЭДС;

Um,Im,Em - амплитудные значения, т.е. наибольшие значения гармонической функции;

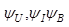-начальная фаза напряжения,тока и ЭДС.

w-круговая частота,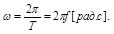

f-частота ,

Начальная фаза характеризует значение напряжения ( тока, ЭДС ) в начальный (нулевой) момент времени.

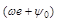- фаза характеризует значение напряжения (тока, ЭДС) в данный момент времени

При анализе цепей гармонического тока большое значение имеют не начальные фазы напряжений и токов, а их разность, которая называется углом сдвига фаз (фи). 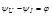(см. рис 2.3)

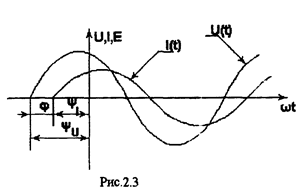
В случае, если:

1) 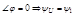,т.е. ток и напряжение совпадают по фазе;

2) 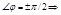ток и напряжение расположены под углом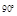

3) 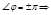ток и напряжение находятся в противофазе.

2.2 Действующее и среднее значение гармонического тока.

Действующее (эффективное) значение - это среднеквадратичное значение переменного

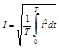
Действующее значение характеризует тепловое воздействие переменного тока. Действующее значение периодического тока числено равно такому постоянному току, который за время равное периоду переменного тока выделяет такое же количество тепла, что и переменный ток.

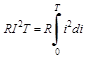
Найдем действующее значение гармонического тока: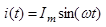

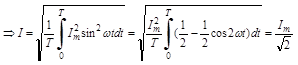
Так как 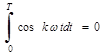,то взяв интеграл, получим:

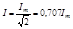А

Найдем среднее значение. Как известно из математики, среднее значение равно высоте прямоугольника, равновеликого по площади, под данной кривой, т.е.

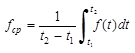
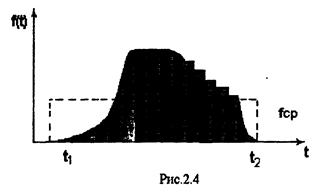
Определим среднее значение для гармонического тока. Так как за период имеется положительная и отрицательная полуволна (см. рис. 2.2), то среднее значение гармонического тока за период равно нулю, следовательно определяем его за полупериод.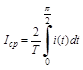

Среднее значение тока Iср характеризует заряд, который переносит

переменный ток за время, равное половине периода. Поэтому среднее значение гармонического тока определяют следующим образом:

Iср равно такому постоянному току, который за время , равное T/2

переменного тока переносит такой же заряд, что и постоянный ток.

Определим, как связаны амплитудное и среднее значение для гармонического тока.

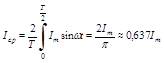
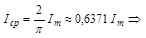среднее значение, обычно меньше действующего Iср < I Для характеристики кривых вводятся коэффициенты

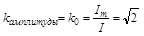
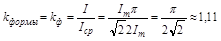
2.3. Изображение синусоидальных величин с помощью вращающихся векторов. Метод комплексных амплитуд.

При анализе цепей необходимо выполнять операции над гармоническими функциями по правилам тригонометрии, что вызывает затруднения, поэтому сначала было предложено изображать гармонические функции в виде

проекции вращающегося вектора на ось абсцисс или ординат, а затем использовать метод комплексных амплитуд.

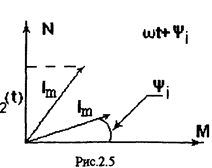
Покажем, что гармоническую функцию можно определить в виде проекции вращающегося вектора. Возьмем оси М, N прямоугольной системы координат и в момент времени t=0 изобразим вектор, равный амплитудному значению Im и образующий угол (gcb)I с осью М. Пусть

данный вектор вращается против часовой стрелки с угловой скоростью (омега). Тогда в момент времени t он займет положение под углом ((омега)t +(пси)I).

Рассмотрим проекцию данного вектора на ось ординат. Она равна

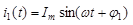,т.е.

гармоническую функцию можно представить в виде вектора, вращающегося с угловой скоростью (омега)

Операции с гармоническими функциями при использовании вращающегося вектора заменяются операциями над векторами (векторная алгебра).

Возьмем комплексную плоскость и изобразим комплексное число А (см. рис. 2.6)

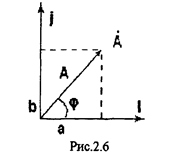
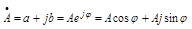,где j=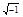

Модуль А и аргумент комплексного числа (фи) связаны с вещественной a и мнимой b частями комплексного числа выражениями:

A= 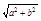; 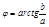(Ф-лы перехода от алгебраической к показательной форме записи

Вспомним основные операции с комплексными числами:

В соответствии с ф-лами Эйлера: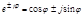

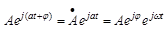
1) 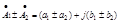- сложение

2) 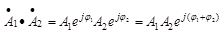-умножение

3) 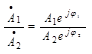-деление.

А* - число, сопряженное с числом А, если оно отличается знаком у мнимой части, либо знаком у аргумента.

Произведение комплексного числа А на сопряженное А* равно квадрату модуля.

Изобразим вращающийся вектор в комплексной плоскости. Конец вектора определяет некоторую точку, т.е комплексное число.

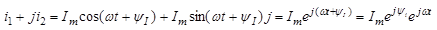
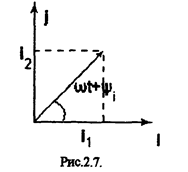
Обозначим -комплекс амплитудного знач-я тока

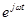-множитель вращения

С учетом введенных обозначений

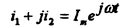
Так как проекция вращающегося вектора на ось ординат представляет временную функцию, то

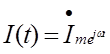
прямое преобразование, т.е. синусоидальной функции можно поставить в соответствие комплексное число (амплитуду).

Пример: 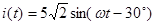-мгновенное значение (оригинал )

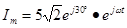-комплекс амплитудного значения тока (изображение)

Часто множитель вращения опускают и записывают только комплексную амплитуду. Например

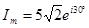
Так как амплитудное и действующее значения связаны (корень из 2) , то можно определить комплекс действующего значения тока

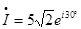
При анализе цепей возможно пользоваться комплексом либо амплитудного, либо действующего значения тока (напряжения, ЭДС).

Обратное преобразование осуществляется в соответствии с выражением -получается

синусоидальная функция времени.

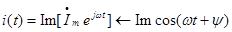-получается

косинусоидальная функция времени.

Пример: 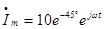,тогда мгновенное значение тока л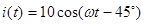ибо ,либо 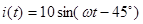в зависимости от того какую через функцию определяется мгновенное значение.

Свойства метода комплексных амплитуд (МКА).

1) Свойство линейности.

Изображение суммы оригиналов равняется сумме изображений.

Оригинал - i(t); изображение — комплексная амплитуда.

;

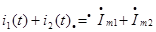
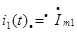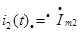
Следствие из свойства линейности :пусть 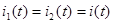,тогда

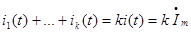
При умножении оригинала на постоянный множитель, изображение также умножается на постоянный множитель.

2) Изображение производной

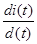
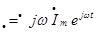
Изображение производной оригинала соответствует изображению, умноженному на множитель j(омега)

3) Изображение интеграла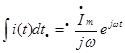

Изображение интеграла от оригинала соответствует изображению, деленному на множитель j(омега).

Свойства 2) и 3) определяют достоинства МКА, a именно: интегрально-дифференциальные уравнения, которые описывают электромагнитные процессы в цепи, относительно мгновенных значений заменяются алгебраическими уравнениями относительно комплексных амплитуд, решение которых значительно упрощается.

2.4. Параметры цепей гармонического тока.

Так как в цепи гармонического тока и токи, и напряжения изменяются во времени, то для цепи переменного тока существует 4 параметра:

R- сопротивление;

L- индуктивность;

С- емкость;

М - взаимная индуктивность, которые определяют режим работы цепи. Рассмотрим следующие параметры.

Индуктивность L

Индуктивность - это такой идеальный элемент электрической цепи, в котором энергия источника запасается в виде энергии магнитного поля. Условное обозначение:

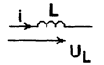
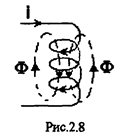
Реальным устройством, обладающим такими свойствами является индуктивная катушка (рис.2.8). Пусть в катушке протекает ток i. Тогда будет создано магнитное поле, которое характеризуется магнитным потоком Ф. Направления тока i и магнитного потока Ф связаны правилом буравчика (винта), иначе правилом правой руки

Потокосцепление - это произведение потока на число витков: Фw=(пси) , где w - число витков.

Как известно, индуктивность, как величина, определяется отношением потокосцеппения самоиндукции к току, его вызвавшему, т.е.

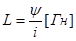
Индуктивность не зависит ни от потокосцепления (пси), ни от i, a определяется:

;

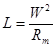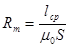
где 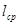-средняя длина пути замыкания потока самоиндукции;

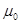-абсолютная магнитная проницаемость пути замыкания потока самоиндукции .

S-площадь поперечного сечения магнитного сердечника.

Найдем ЭДС самоиндукции. В соответствии с законом электромагнитной индукции:

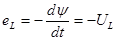
ЭДС самоиндукции еL уравновешивается напряжением самоиндукции uL -Тогда:

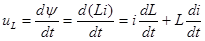-равно 0 для линейной цепи

U 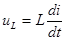-напряжение самоиндукции.

Определим мгновенную мощность:

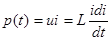,знак мощности определяется знаком

производной, т.е.если i возрастает, то p(t)>0 - происходит накопление энергии в магнитном поле.

если i убывает, то p(t)<0- энергия рекуперируется в источник если i постоянен, то p(t)=0.

Таким образом в индуктивности происходит колебание энергии (см. Колебание энергия). В течении половины периода мощность от источника накапливается в магнитном поле индуктивности , а затем в другой полупериод возвращается в источник . Активная мощность при этом равна нулю

-27-Емкость С

Емкость - это идеальный элемент цепи, в котором энергия источника запасается в виде энергии электрического поля.

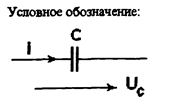
Реальное устройство - конденсатор.

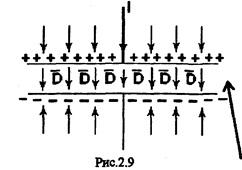
D - вектор электрического смещения, введен Максвеллом и характеризует ток смещения, (протекает в диэлектрике). Считаем что ток проводимости

численно равен току смещения, тогда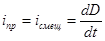

Вектор электрического смещения связан с напряженностью поля

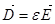,где 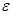-диэлектрическая проницаемость

E-напряжённость электрического поля

Найдем ток в емкости. Как известно, емкость есть отношение заряда к напряжению:

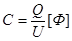
Емкость не зависит ни от заряда Q, ни от напряжения U, а определяется диэлектрической проницаемостью среды (е) и геометрическими размерами:

площадью S и расстоянием между пластинами d Например, для плоского конденсатора его емкость равна

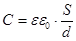,где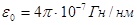

Как известно, ток i связан с зарядом Q.

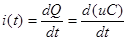
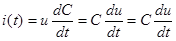
Для линейных цепей C=const, поэтому первое слагаемое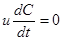

Зная ток, всегда можно найти напряжение:

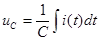
Определим мгновенную мощность:

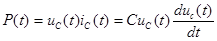
Аналогично, как и в индуктивности. Имеют место колебания энергии между электрическим полем и источником (см.Колебания энергия).