Вихревые токи. Скин-эффект

Токами Фуко, или вихревыми токами, называют индукционные токи, возбуждаемые в сплошных массивных проводниках. Так как сопротивление массивного проводника мало, то вихревые токи могут достигать очень большой силы. Они подчиняются правилу Ленца – их направление в проводнике таково, что они препятствуют причине, их вызывающей. Поэтому движущиеся в квазистационарном поле сплошные проводники затормаживаются за счет взаимодействия токов Фуко с магнитным полем. Этим пользуются для демпфирования подвижных частей измерительных приборов. Тепловое действие вихревых токов используется в индукционных печах.

Во многих случаях вихревые токи бывают вредными. Так, теплота, выделяемая токами Фуко в сердечниках трансформаторов, представляет собой потери трансформируемой энергии. Для уменьшения потерь увеличивают сопротивление сердечников, набирая их из отдельных листов.

Вихревые токи, возникающие в проводах, по которым текут квазистационарные токи, направлены так, что ослабляют ток внутри провода и усиливают вблизи поверхности (рис. 105.1). В результате переменный ток оказывается распределенным по сечению провода неравномерно – он как бы вытесняется на поверхность проводника. Это явление называется скин-эффектом, или поверхностным эффектом.

Уменьшение плотности тока по мере приближения к оси проводника означает в соответствии с законом Ома (54.7), что напряженность электрического поля максимальна у поверхности и минимальна на оси. Глубину проникновения (т. е. расстояние, на котором плотность тока во много раз меньше, чем на поверхности) можно оценить на основе несложных расчетов. Рассмотрим два прямоугольных контура, плоскости которых взаимно перпендикулярны (рис. 105.2). Контур 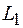со сторонамиa и 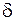расположен в продольном сечении проводника; одна сторона на поверхности, остальные – внутри проводника, причем сторона 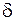равна глубине проникновения тока. Циркуляция вектора 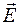для этого контура равна 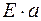, поскольку на двух других сторонах вектор 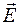перпендикулярен участкам контура, а на третьей .

С другой стороны, согласно формуле (97.1) .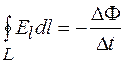

Отсюда следует соотношение

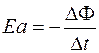. (105.1)

За половину периода 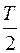поток меняется от Ф до 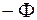, т. е. 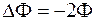и 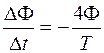. Заменяя 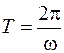, где 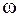– циклическая частота переменного тока, получим:

.

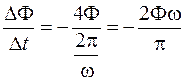В свою очередь, 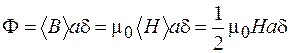(Н – напряженность магнитного поля у поверхности, 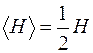). Тогда

.

После подстановки этого соотношения в формулу (105.1) получаем 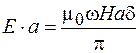. Отсюда следует:

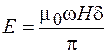. (105.2)

Значение напряженности магнитного поля Н у поверхности проводника найдем, применив закон полного тока (71.4) для контура :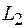

,

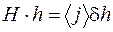откуда

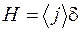. (105.3)

По закону Ома 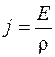и 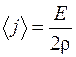. Тогда из выражения (105.3) найдем:

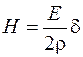. (105.4)

Подставив выражение (105.4) в формулу (105.2), получим:

.

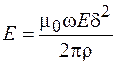Отсюда выразим глубину проникновения тока (и поля):

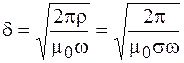. (105.5)

Из выражения (105.5) следует, что глубина проникновения электромагнитного поля в вещество обратно пропорциональна корню квадратному из его проводимости и частоты. Вывод этой формулы не является строгим, но она дает верное по порядку значение глубины проникновения тока.

Для меди ( 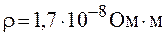) из формулы (105.5) получаем:

а) при 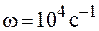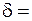2,8 мм;

б) при 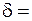0,28 мм.

Из-за поверхностного эффекта внутренняя часть проводников при высоких частотах оказывается бесполезной. Поэтому в высокочастотных цепях применяют проводники в виде трубок. Вологдин В. П. предложил использовать токи высокой частоты для поверхностной закалки деталей машин. Меняя частоту тока, можно производить закалку на любую необходимую глубину.