Вихревые движения жидкости
Различают два значения термина «вихрь» – физический вихрь и расчётный вихрь.
Физическим вихрем называют группу частиц жидкости, вращающихся вокруг одной мгновенной оси с одинаковой угловой скоростью (как твердое тело). Мгновенная ось вращения может быть неподвижной или перемещающийся в пространстве. В потоке жидкости вихри с неподвижной осью образуются, например, за плохо обтекаемым телом: на рис. 10.1 – вихри за круговым цилиндром, на рис. 10.2 – за корабельным рулём.

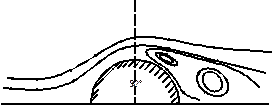 |
Рис. 10.1 Рис. 10.2
Система физических вихрей, расположенных непрерывно вдоль одной общей оси вращения, называетсявихревым шнуром. По длине вихревого шнура угловая скорость вращения может изменяться, но в каждом сечении шнура, нормальном к его оси, частицы жидкости вращаются с одинаковой угловой скоростью. В общем случае вихревой шнур может перемещаться в пространстве и изменять свою форму, но так, чтобы касательная к оси шнура совпадала с направлением угловой скорости вращения частиц жидкости.
Главной характеристикой вихревого шнура является его напряжение 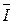 ,которое равно произведению угловой скорости вращения
,которое равно произведению угловой скорости вращения 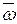 на нормальную к ней площадь сечения шнура
на нормальную к ней площадь сечения шнура 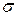
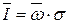 . (10.1)
. (10.1)
Если сечение вихревого шнура бесконечно мало, то такой вихревой шнур называется элементарным. Его напряжение обозначают через 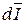 и считают, что
и считают, что
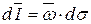 .
.
В отличие от конечных (сосредоточенных) вихревых шнуров элементарные вихревые шнуры располагаются в потоке жидкости непрерывно, заполняя определённые его области (например, в пограничном слое).
Расчётным вихрем называют вектор угловой скорости вращения частиц жидкости 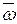 (проекции его на оси декартовой системы определяются по (9.5)). Так как эти зависимости выражаются через производные от проекций линейной скорости, которая является функцией координат, то в вихревом потоке вместе с векторным полем линейной скорости
(проекции его на оси декартовой системы определяются по (9.5)). Так как эти зависимости выражаются через производные от проекций линейной скорости, которая является функцией координат, то в вихревом потоке вместе с векторным полем линейной скорости 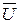 в каждый момент времени имеется и векторное поле угловой скорости
в каждый момент времени имеется и векторное поле угловой скорости 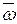 .
.
Возникновение завихренности в идеальной (невязкой) жидкости связывается с образованием и распадом так называемых поверхностей раздела.
Такого рода поверхности могут возникнуть, например, при слиянии двух потоков позади ребра острого двугранного угла (рис. 10.3), если скорости потоков до их слияния отличаются по величине или направлению. В непосредственной близости позади ребра на поверхности раздела имеет место скачок скорости.



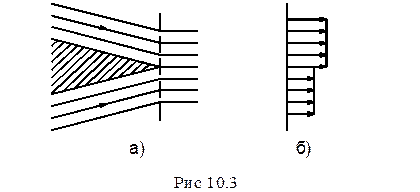 |
В результате воздействия какого-нибудь случайного возмущения поверхность раздела начинает искривляться, принимая волнообразную форму. В дальнейшем деформация поверхности раздела нарастает; постепенно она закручивается, образуя вихрь с осью вращения, параллельной ребру угла. Затем этот вихрь под воздействием потока открывается и уплывает вниз по течению, а на его месте образуется новый.
Подобную же картину образования и распада поверхности раздела и появления вихрей можно наблюдать при обтекании потоком острого угла (рис. 10.4)
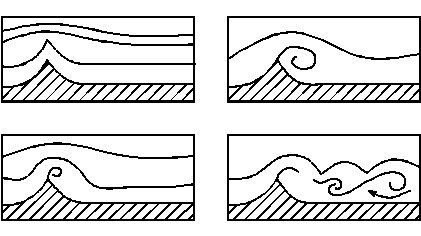 |
Рис. 10.4
При этом в потоке позади ребра появляется круговое движение, вследствие чего жидкость в этой зоне начнет притекать к ребру в направлении, противоположном потоку. Таким образом, около ребра будет происходить слияние двух струй, имеющих различные скорости. На границе струй появится поверхность раздела, которая под действием вихря начнет совместно с ним закручиваться; вихрь при этом начнет увеличиваться в размерах. Со временем под воздействием набегающего потока наступает разрыв поверхности раздела, после чего свободный вихрь уплывает вниз по течению, а на его месте возникает новый.
Задача 10.1. В прямой круглой трубе радиуса 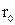 существует ламинарный режим движения. Во всех точках потока скорость направлена вдоль оси трубы и распределена по сечению по параболическому закону
существует ламинарный режим движения. Во всех точках потока скорость направлена вдоль оси трубы и распределена по сечению по параболическому закону
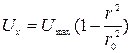 ,
, 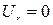 ,
,
где 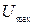 – скорость на оси трубы;
– скорость на оси трубы; 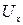 – скорость на расстоянии r от оси.
– скорость на расстоянии r от оси.
Определить, является ли такой поток вихревым.
Решение.Направим ось ОХ декартовой системы вдоль оси трубы; тогда
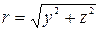
и формулы для составляющих скорости примут вид
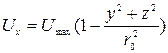 ,
, 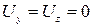 .
.
В данном случае
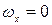 ,
, 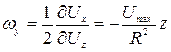 ,
, 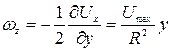 .
.
Величина вектора угловой скорости равна
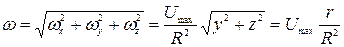 ;
;
она пропорциональна скорости на оси трубы, равна нулю на оси трубы и достигает максимума на стенках.
Так как вектор 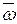 лежит в плоскости поперечного сечения трубы
лежит в плоскости поперечного сечения трубы 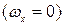 , то направление его определяется углом, который он образует, например, с осью Y.
, то направление его определяется углом, который он образует, например, с осью Y.
Дата добавления: 2015-08-01; просмотров: 2056;
