Примеры плоских сечений

Пример Д.2.1. Рассмотрим плоское прямолинейное и равномерное установившееся течение несжимаемой невязкой жидкости с одинаковой во всём потоке (в любой точке) скоростью, направленной вдоль оси Оy. В этом случае

,

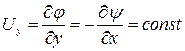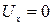
Тогда уравнение неразрывности удовлетворяется, и течение является потенциальным.

Тогда

–

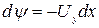
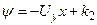линии равных потенциалов 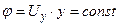представляют собой прямые, параллельные оси абсцисс, рис. Д.2.3. Ось Оy (x=0) также является одной из эквипотенциальных линий; обозначим её через .

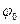Рис. Д.2.3

Для функции тока найдём аналогично

.

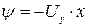Линии тока представляют прямые, параллельные оси Оy.

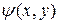Задача Д.2.2.Найти потенциал и функцию тока плоского поступательного потока, направленного под углом к оси абсцисс.

Решение.Такой поток может быть образован в результате наложения плоского однородного поступательного потока, параллельного оси абсцисс на плоский однородный поступательный поток вдоль оси ординат.

, .

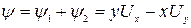Пример Д.2.2. Предположим, что невязкая несжимаемая жидкость непрерывно подводится к некоторой точке плоскости и растекается по ней с одинаковой интенсивностью по всем направлениям, рис. Д.2.4; такое течение называется плоским источником.

Проведём из центра источника несколько концентрических окружностей различного радиуса. Уравнение постоянства расхода через цилиндрическую поверхность, построенную на любой окружности и имеющую высоту, равную единице, будет иметь вид (при 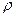=const)

.

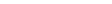Скорость, как следует из последнего равенства, выразится так

,

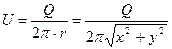где .

Поэтому

.

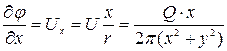Аналогично

;

окончательно полный дифференциал потенциала скорости

.

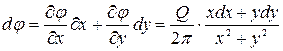Интегрируя это выражение, найдём потенциал скорости для источника

,

где С – константа интегрирования, которую можно принять равной нулю, если положить, что при круге r=1 функция и тогда

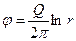, (Д.2.10)

Для определения функции тока учтём, что

, ,

.

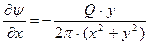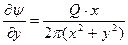После интегрирования

.

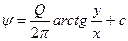Из рис. Д.2.4 видно, что 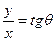, где – угол, образованный одной из линий тока. Принимая 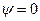, при y=0 получаем c=0 и, следовательно, для функций тока можно записать

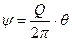. (Д.2.11)

Эта зависимость выражает функцию тока источника. Из выражений (Д.2.10) и (Д.2.11) следует, что потенциал скорости источника может быть представлен семейством концентрических окружностей различного радиуса, а функция тока 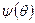представляется пучком прямых, исходящих из центра.

Потенциал скорости и функция тока для стока будут иметь вид, аналогичный (Д.2.10) и (Д.2.11), но с обратным знаком, т.е.

, .

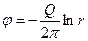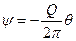Пример Д.2.3. Рассмотрим течение, которое получается при одновременном существовании (наложении) на некотором расстоянии друг от друга источника и стока равной интенсивности (равного радиуса). Начало координат поместим в точку, делящую расстояние между центрами источника и стока пополам. Допустим, что источник располагается в точке 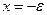, а сток в точке 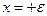, рис. Д.2.5. В этом случае потенциалы скорости и функции тока для источника и стока определяются следующими зависимостями

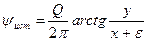, ; (Д.2.12)

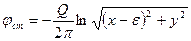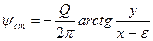, . (Д.2.13)

Будем теперь сближать источник и сток, т.е. величина 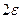стремится к нулю . В пределе при сток поглотит источник и всякое движение будет отсутствовать. Если одновременно со сближением центров источника и стока будем увеличивать их расход так, чтобы

,

то получим в процессе течение, которое называется диполем. Постоянная М, характеризующая этот поток, называется моментомдиполя, а ось Оx – осью диполя. На основании зависимостей (Д.2.12) и (Д.2.13) определяем потенциал скорости и функцию тока рассматриваемого течения (диполя) так, как будет показано ниже.

=

.

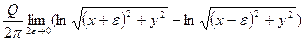Умножим числитель и знаменатель последнего равенства на 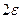; в числителе получим , т.е.

.

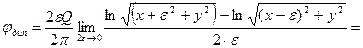
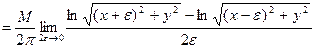В последнем выражении – предел отношения приращения функции к приращению аргумента по координате х, что является частной производной по х; поэтому выражение для может быть записано так

.

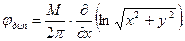Аналогично для функции тока диполя получается выражение

.

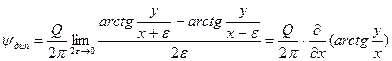Выполняя операции дифференцирования, приходим к окончательным выражениям

,

.

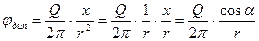Анализ последних уравнений показывает следующее: линии тока диполя есть окружности, проходящие через начало координат и имеющие центры на оси Оу, рис. Д.2.6; эквипотенциальные линии также представляют собой окружности, проходящие через начало координат, но с центрами, расположенными на оси ОХ. Жидкость движется из начала координат в сторону отрицательного направления оси Ох и, описав окружность, снова попадает в начало координат. Течение жидкости в диполе – идеализированное, не встречающееся на практике, но изучение его позволяет построить схемы течений некоторых реальных потоков.

Пример Д.2.4. Бесциркуляционное обтекание круглого цилиндра плоским прямолинейным потоком.

Рассмотрим цилиндр бесконечной длины, который обтекается безграничным прямолинейным плоским потоком идеальной жидкости перпендикулярно его оси и так, что скорость набегающего потока 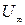направлена вдоль оси Ох; начало координат поместим на оси цилиндра. Произведём сложение двух течений: одного – диполя, помещённого в начале координат, а второго – прямолинейного со скоростью , параллельной оси ОХ. Произведём суммирование функций тока

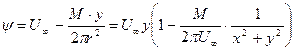. (Д.2.14)

Из этого равенства следует, что при у=0, а также на окружности радиуса 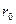, определяемого условием

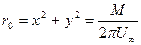, (Д.2.15)

функция тока равна нулю, т.е. постоянна и, следовательно, названные линии являются линиями тока. Картина линий тока приведена на рис. Д.2.7.

Так называемая «нулевая» линия тока 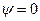состоит из отрезка отрицательной оси абсцисс от бесконечности до точки А, из окружности радиуса 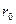(ACBD) и из отрезка положительной оси абсцисс от точки В до бесконечности. Эта «нулевая» линия тока разграничивает две области течения жидкости: «внешний поток» (вне окружности радиуса 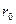) и «внутренний поток», замыкающийся внутри окружности радиуса 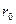. Этот «внутренний поток» не влияет на поведение внешнего потока и ,следовательно, картина обтекания не изменится, если предположить, что потоком обтекается жесткий цилиндр радиуса 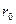. Такое течение носит название бесциркуляционного обтекания цилиндра. Исключая с помощью (Д.2.15) момент диполя из (Д.2.14), найдём выражение для функции тока (при )

.

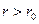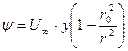Потенциал скорости такого течения будет иметь вид

.

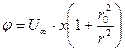Формулы перехода от прямоугольных координат (х,у) к полярным имеют вид

,

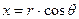и, следовательно, функци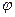и и могут быть представлены в полярных координатах

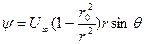, (Д.2.16)

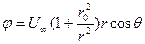. (Д.2.17)

Найдём распределение скоростей по контуру цилиндра. Для этого достаточно найти тангенциальную составляющую 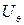, так как скорость направлена по касательной к линии тока, а радиальная составляющая скорости на контуре цилиндра равна нулю. Поэтому

.

Знак «минус» указывает, что скорость направлена в сторону, противоположную направлению отсчёта углов 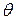. Распределение скоростей по развёртке полуокружности (верхней и нижней) имеет вид отрезка синусоиды. Скорости в точках А и В – так называемых точках разветвления (критических точках) – пр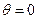и и 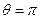равны нулю. Максимум скорости достигается на пересечении поверхности цилиндра с осью ординат

,

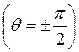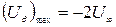. (Д.2.18)

Задача Д.2.3.применяя зависимость (Д.2.16), построить линии тока для случая обтекания цилиндра при следующих данных: r=3 см, 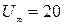см/с. Построить кривую распределения скорости 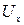на осевом сечении цилиндра от его поверхности (по вертикали от точки С, рис. Д.2.6).