Ая, 2-ая, 8-ая и 16-ая системы как примеры позиционных систем
При работе с компьютером приходится параллельно использовать несколько позиционных систем счисления (чаще всего двоичную – т.к. внутреннее представление информации в компьютере является двоичным, десятичную – т.к. мы привыкли к этой системе со школы и шестнадцатеричную – для сокращения записи чисел). Поэтому большое практическое значение имеют процедуры перевода чисел из одной системы счисления в другую. Обратите внимание, что во всех приведенных примерах результат является десятичным числом. Таким образом, представляя число в виде суммы произведений коэффициентов на степени основания, можно перевести число из любой системы счисления в десятичную.
Целая и дробная части десятичного числа переводятся порознь.
Чтобы перевести целую часть числа из десятичной системы счисления в систему с основанием В, необходимо разделить ее на В. Остаток даст младший разряд числа. Полученное при этом частное необходимо вновь разделить на В – остаток даст следующий разряд числа и т.д. Деление производят до тех пор, пока частное от деления не станет меньше основания В. Последнее частное, будет самым старшим разрядом числа.
Примеры: Остаток
25:2=12 (1)
12:2=6 (0)
6:2=3 (0)
3:2=1 (1)
Значения получившихся остатков, взятые в обратной последовательности, образуют искомое двоичное число.
Таким образом, 25(10) = 11001(2)
125(10)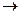 
X(8) = 175(8)
125:8=15 (5)
15:8=1 (7)
1234(10) 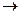Х(16) =4DC(16)
1234:16=77 (12) С
77:16=4 (13) D
Для перевода дробной части ее необходимо умножить на В. Целая часть полученного произведения будет первым (после запятой) знаком. Дробную же часть произведения необходимо вновь умножить на В. Целая часть полученного числа будет следующим знаком после запятой и т.д. до нужного количества знаков после запятой.
Например:
0,73*2=1,46 (целая часть 1),
0,46*2=0,92 (целая часть 0),
0,92*2=1,84 (целая часть 1),
0,84*2=1,68 (целая часть 1) и т.д.
В итоге 0,73(10) = 0,1011…(2).
С точки зрения изучения принципов представления информации, в компьютере системы счисления представляют большой интерес. Хотя компьютер «знает» только двоичную систему счисления, часто с целью уменьшения количества записываемых на бумаге или вводимых с клавиатуры знаков бывает удобнее пользоваться восьмеричными или шестнадцатеричными числами. С практической точки зрения представляет интерес процедура взаимного преобразования двоичных, восьмеричных и шестнадцатеричных чисел. Для этого используется таблица соответствия чисел в различных системах счисления (Таблица 2).
Таблица 2.
Дата добавления: 2015-08-08; просмотров: 1253;