Д.2. Плоские течения

Рассмотрим частный, но практически важный случай плоского течения несжимаемой жидкости, т.е. такого, в котором: a ) конфигурация линий тока во всех плоскостях, нормальных некоторой прямой, одинакова; б) все линии тока являются плоскими кривыми, лежащих в этих плоскостях.

Изучение плоских течений по сравнению с пространственными значительно облегчается, во-первых, потому, что уравнения, их описывающие, содержат две переменных, а во-вторых, потому, что достаточно изучить течение всего лишь в одной плоскости, чтобы составить представление о потоке в целом. В дальнейшем рассматриваются только установившиеся течения.

Д.2.1. Функция тока

Рассмотрим течение жидкости, при котором распределение скоростей зависит только от двух координат, например от x и y, причём скорость параллельна везде плоскости XOY. Для решения задач о двумерном течении несжимаемой жидкости иногда бывает удобным выражать скорость через так называемую функцию тока. Из уравнения неразрывности

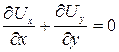(Д.2.1)

видно, что компоненты скорости могут быть представлены в виде производных

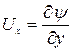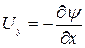, (Д.2.2)

от некоторой функции 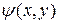, называемой функцией тока. Уравнение неразрывности при этом удовлетворяется автоматически.

Зная функцию тока, можно непосредственно определить форму линий тока для установившегося движения жидкости. Дифференциальное уравнение линий тока (при двумерном течении) есть

(Д.2.3)

или 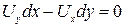; оно выражает собой тот факт, что направление касательной к линии тока в каждой точке совпадает с направлением скорости. Подставляя в последнее уравнение (Д.2.2), получаем

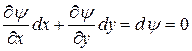, (Д.2.4)

откуда

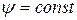. (Д.2.5)

Таким образом, линии тока представляют собой семейство кривых, получающихся приравниванием функции тока 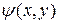произвольной постоянной.

При установившемся течении каждая линия тока не меняет своей формы и может быть заменена твёрдой стенкой. Зная функцию тока течения, можно указать формы линий тока и, следовательно, формы стенок, которые могут обтекаться при этом течении.

Таким образом, альтернативно вектор скорости можно представить через функцию тока, чьё существование есть следствие уравнения неразрывности. С математической точки зрения функцию тока можно рассматривать как одно из общих решений уравнения неразрывности движения для плоского потока.

Из предыдущего можно сделать вывод, что функция тока существует независимо от того, вихревым или потенциальным является движение жидкости. Если проекции вектора скорости определяются как в (Д.2.2), то уравнение неразрывности выполняется автоматически. Покажем, что если поток потенциальный, то функция тока удовлетворяет уравнению Лапласа. Если поток потенциальный, то 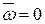и

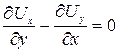. (Д.2.6)

Подставляя в (Д.2.6) значения 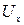и из (Д.2.2) получаем

, (Д.2.7)

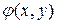т.е. уравнение Лапласа для . Следовательно, в плоском потенциальном потоке потенциал скорости и функция тока удовлетворяют уравнению Лапласа. Оно обладает свойством линейности: если имеются функци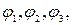и или 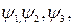…., такие, что каждая из них в отдельности удовлетворяет уравнению Лапласа, то ему будут удовлетворять также и линейные комбинации, т.е. функции вида

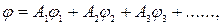
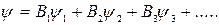
где 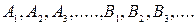– постоянные числовые коэффициенты . Таким образом, при наложении одного такого потенциального потока на другой потенциальный поток, полученный в результате сложения, будет также потенциальным и его потенциал скорости и функция тока будут определяться путём алгебраического суммирования значений потенциалов и функцией тока исходных потоков. Заметим, что потенциальные (безвихривые) потоки, которые в природе не существуют, могут быть как плоскими, так и пространственными. Функция тока, хотя и может быть введена только для плоского (или осесимметричного) потока и зависит от двух координат, может описывать как потенциальные, так и вихревые движения.

Связь между потенциалом скорости и функцией тока устанавливается путём сопоставления зависимостей (9.7) и (Д.2.2)

, ,

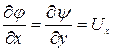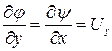т.е. 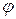и 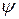с точностью до произвольной постоянной однозначно связаны между собой и полностью определяет поле скоростей.

Задача Д.2.1. Представляют ли выражения

,

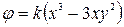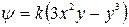
соответственно потенциал скорости и функцию тока одного и того же течения? Постоянная k имеет размерность 1/Lt.

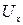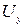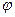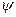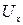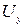Решение. Для ответа на вопрос, поставленный в задаче необходимо найти проекции скорости и исходя вначале из потенциала скорости, а затем найти те же проекции, исходя из выражения для функции тока. Дифференцируя и , убеждаемся, что в обоих случаях и полностью совпадают и ответ на вопрос задачи положительный.

Д.2.2. Сетка течения плоского потенциального потока

несжимаемой жидкости

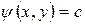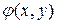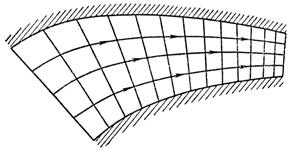
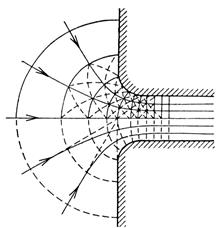
Система линий тока (уравнение каждой линии имеет вид ) позволяет наглядно представить поток, сделать необходимые оценки и определить многие величины. Такая система линий тока является во многих случаях необходимым геометрическим образом. Независимо от функции тока можно найти потенциал скорости и, следовательно, эквипотенциальные линии (линии равного потенциала) 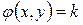, которые также можно построить в плоскости течения, рис. Д.2.1 и Д. 2.1, б.

Рис. Д.2.1

При совместном построении линий тока и эквипотенциальных линий возможно выявить важные для дальнейшего свойства, а именно: эти семейства (системы этих линий) образуют ортогональную сетку плоского течения.

Рассмотрим потенциальное течение в плоскости xoy и напомним, что вектор скорости 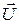совпадает с направлением касательной в любой точке линии тока и образует с осью абсцисс некоторый угол α. Если учесть уравнение линии тока

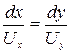или ,

то тангенс угла

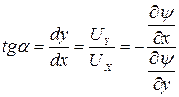. (Д.2.8)

Для линии равного потенциала 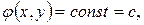проходящую через ту же точку можно записать

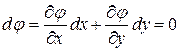(Д.2.9)

С учётом того, что геометрический смысл производной 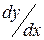представляет собой тангенс угла наклона касательной к кривой в данной точке, последнее равенство переписывается так

;

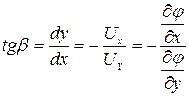напомним, что 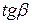-тангенс угла, образованного касательной к линии равного потенциала и осью абсцисс. Перемножая (Д.2.8) и (Д.2.9), получим

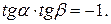
Известно, что этому условию отвечают угловые коэффициенты взаимно перпендикулярных линий.

На рис. Д.2.1, а изображена сетка течения в напорном плоском канале переменного сечения, а на рис. Д.2.1, б – втекание жидкости из резервуара в плоский напорный канал.