Д.1. Уравнения линий тока
Построение линий тока является одним из средств наглядного изображения особенностей течения. Поверхность тела, непроницаемую для жидкости, возможно представить состоящей из линий тока. Например, при плоском обтекании препятствия на дне канала сама твёрдая граница будет линией тока, рис.Д.1.1,которая часто называется нулевой. В общем случае через любую точку движущейся среды в данный момент времени можно провести лишь одну линию тока, но существуют некоторые особые точки, в которых это правило нарушается. В особых точках линии тока пересекаются, следовательно, в этих точках вектор скорости имеет разные направления, что при конечном значении скорости невозможно. Поэтому в особых точках величина скорости должна быть равна либо нулю, либо бесконечности. При обтекании тела нулевая линия тока, образующая непроницаемый контур, имеет особые точки А и A1, рис. Д.1.2. В этих точках, называемых критическими, величина скорости равна нулю.
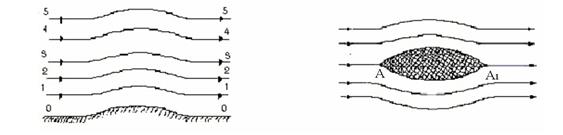
Рис. Д.1.1 Рис. Д.1.2
Предположим, что поле скоростей потока известно и необходимо найти линии тока. По определению вектор скорости направлен по касательной к линии тока. Выделим на ней элемент дуги 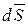 , проекции которого на оси координат обозначим через dx, dy, dz. Так как вектор скорости
, проекции которого на оси координат обозначим через dx, dy, dz. Так как вектор скорости 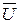 и вектор
и вектор 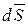 параллельны, то векторное произведение их равно нулю
параллельны, то векторное произведение их равно нулю
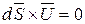 .
.
Записывая это равенство с помощью определителя третьего порядка
 ,
,
находим, что элементы второй и третьей сторон пропорциональны
 . (Д.1.1)
. (Д.1.1)
Таким образом, задача об определении линий тока по заданному полю скоростей сводится к интегрированию системы дифференциальных уравнений. Практическая польза выведенных уравнений состоит в возможности решения (Д.1.1) и получения уравнений линий тока для описания течений жидкости; для этого необходимо знать выражение для проекций скоростей на оси координат.
Введённое ранее в основной части представление о потенциале скорости возможно обобщить, обращая внимание на то, что соотношение
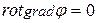
является векторным тождеством и выполняется всегда. Поэтому если
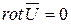 ,
,
то вектор 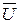 возможно подставить в виде градиента от некоторой скалярной функции
возможно подставить в виде градиента от некоторой скалярной функции 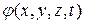 , т.е.
, т.е.
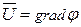 .
.
Из последнего выражения следует, что
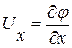 ,
, 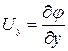 ,
, 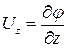 .
.
Задача Д.1.1. Даны зависимости для проекций скорости плоского течения
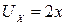 ,
, 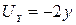 .
.
Выполнить анализ особенностей этого течения, найти уравнение линий тока и выражение для потенциала скорости.
 Решение. Уравнение неразрывности принимает вид 2-2 =0, т.е. поток существует. Кроме того, он потенциальный, так как
Решение. Уравнение неразрывности принимает вид 2-2 =0, т.е. поток существует. Кроме того, он потенциальный, так как 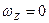 .
.
Уравнение (Д.1.1) в данном случае такое
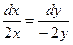 или
или 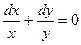 .
.
Интегрируем последнее равенство
 ln x + ln y =ln c или ln(xy)=ln c или xy=c.
ln x + ln y =ln c или ln(xy)=ln c или xy=c.
Окончательно уравнение линий тока
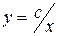 .
.
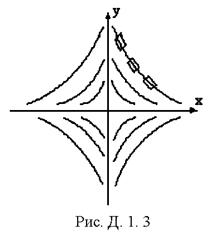
Сами линии тока приведены на рис. Д.1.3.
 Любая частица жидкости движется вдоль кривых линий тока без вращения, так как поток потенциальный. Для нахождения потенциала скорости учтём, что
Любая частица жидкости движется вдоль кривых линий тока без вращения, так как поток потенциальный. Для нахождения потенциала скорости учтём, что
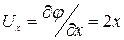 ,
,  .
.
Выражение для 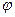 получается из
получается из
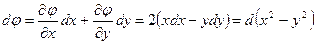 ,
,
откуда 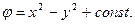
Дата добавления: 2015-08-01; просмотров: 5892;
