Аналитическая геометрия на плоскости. Алгебраические линии и плоскости. Уравнения прямой на плоскости.

Цель: Изучить понятия алгебраической линии и алгебраической поверхности, виды уравнений прямой на плоскости и их основные характеристики.

Определение. Уравнение 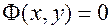называется уравнением линии 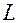на плоскости (относительно заданной системы координат), если этому уравнению удовлетворяют координаты ( 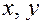) любой точки, лежащей на линии 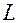, и не удовлетворяют координаты ни одной точки, не лежащей на линиим 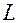. Здесь 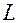- геометрическое место точек, координаты которых удовлетворяют уравнению .

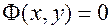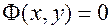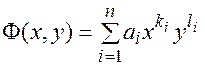Определение: Линия называется алгебраической, если в декартовой прямоугольной системе координат она определяется уравнением , где - алгебраический полином, 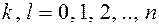- показатели степени все целые неотрицательные числа, 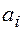- некоторые постоянные.

Определение:Наибольшая из сумм показателей степеней 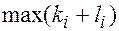называется степенью уравнения или порядком алгебраической линии

Всякая неалгебраическая линия называется трансцендентной.

Определение.Линией -го порядка называется алгебраическая линия, определяемая в декартовой прямоугольной системе координат алгебраическим уравнением -ой степени с двумя неизвестными.

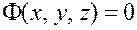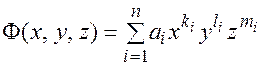Определение: Алгебраической называется множество, которое в какой-либо декартовой прямоугольной системе координат определяется уравнением , где - алгебраический полином, 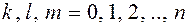- показатели степени все целые неотрицательные числа, 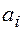- некоторые постоянные.

Определение:Наибольшая из сумм показателей степеней 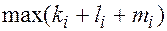называется степенью уравнения или порядком алгебраической поверхности.