Свойства смешанного произведения

1) 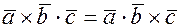, данное свойство позволяет записывать смешанное произведение в виде 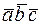. Действительно, из коммутативности скалярного произведения следует, что 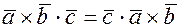, докажем, что 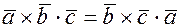, равенство очевидно, поскольку и справа, и слева стоит объем параллелепипеда, построенного на одних и тех же векторах, знаки совпадают, поскольку векторы - имеют одинаковую ориентацию;

2) При перестановки местами двух соседних множителей, смешанное произведение меняет знак на противоположный

.

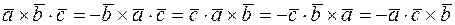Данное свойство следует из антикоммутативности векторного произведения.

3) 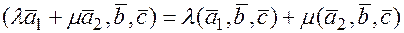. Действительно, т.к. выполняется первое свойство, тогда 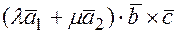, согласно линейным свойствам скалярного произведения, получаем равенство.

Теорема (смешанное произведение векторов в ортонормированном базисе). В ортонормированном базисе 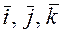смешанное произведение может быть вычислено по формуле:

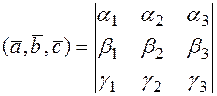(6.6)

Доказательство. Действительно, смешанное произведение равно скалярному произведению векторов и 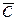, поскольку координаты 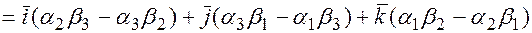, для скалярного произведения векторов в координатах получим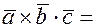 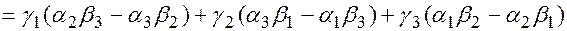= 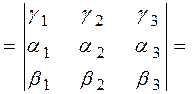(т.к. четное число перестановок не меняет знак определителя) =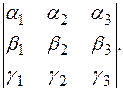

Теорема(о компланарных векторах). Для того, чтобы 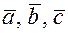были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю, т.е. выполняется равенство:

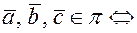
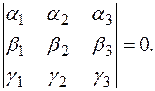(6.7)

В самом деле, если векторы компланарны, то они по определению лежат в одной плоскости или в параллельных плоскостях, следовательно, объем параллелепипеда, построенного на этих векторах, будет равен нулю, учитывая запись смешанного произведения в координатной форме, получаем требуемое равенство. В обратную сторону доказательство аналогично.

Следствие. Смешанное произведение трех векторов два из которых совпадают, равно нулю, например, .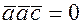

Действительно, поскольку такие векторы заведомо компланарны, их сшешанное произведение будет равно нулю.

Определение. Вектор 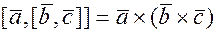– называется двойным векторным произведением.