Свойства векторного произведения
1) 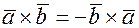 (антикоммутативность)
(антикоммутативность)
Свойство следует из перемены ориентации векторов;
2) Скалярный множитель можно вынести за скобку 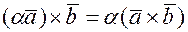 ;
;
3) 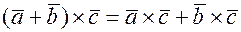 (дистрибутивность);
(дистрибутивность);
4) Векторный квадрат равен нуль-вектору:
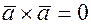 (6.2)
(6.2)
Свойство непосредственно вытекает из определения векторного произведения
Теорема.Чтобы векторы 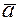 и
и 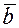 были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулю.
были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулю.
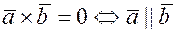 (6.3)
(6.3)
Доказательство. Докажем, что есливекторы коллинеарны, то их векторное произведение равно нулю. Действительно, т.к. векторы 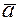 и
и 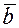 коллинеарны, значит, угол
коллинеарны, значит, угол 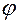 между ними составляет
между ними составляет 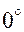 либо
либо 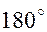 . Тогда
. Тогда 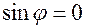 , т.е. длина вектора, полученного в результате перемножения коллинеарных векторов, равна нулю, это возможно только у нулевого вектора.
, т.е. длина вектора, полученного в результате перемножения коллинеарных векторов, равна нулю, это возможно только у нулевого вектора.
Докажем теперь, что если векторное произведение равно нулю, то векторы коллинеарны. Пусть оба вектора 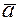 и
и 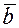 ненулевые (в противном случае доказательство тривиально), тогда
ненулевые (в противном случае доказательство тривиально), тогда 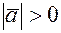 и
и 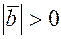 , поэтому
, поэтому 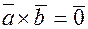 только в том случае, если
только в том случае, если 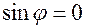 , т.е. векторы
, т.е. векторы  должны быть коллинеарны.
должны быть коллинеарны.
Теорема. В ортонормированном базисе декартовой прямоугольной системы координат 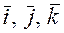 компоненты векторного произведения могут быть вычислены по формуле:
компоненты векторного произведения могут быть вычислены по формуле:
 (6.4)
(6.4)
где 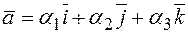 ,
, 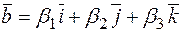 .
.
Доказательство.Поскольку 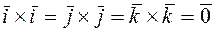 и
и
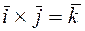 ,
, 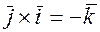 ,
, 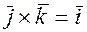 ,
, 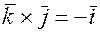 ,
, 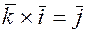 ,
, 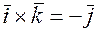
тогда 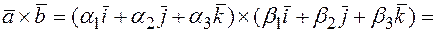
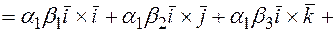
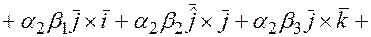
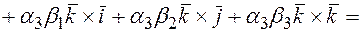
=(учитывая выше записанные равенства, упрощаем полученное выражение)
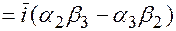

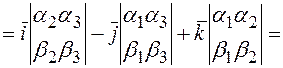
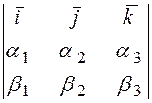 .
.
Вместо 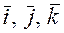 можно взять любой ортонормированный базис.
можно взять любой ортонормированный базис.
Теорема(о коллинеарных векторах). Если два вектора коллинеарны, то их координаты пропорциональны:
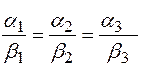 (6.5)
(6.5)
Доказательство. Пусть 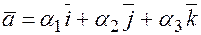 и
и 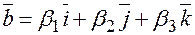 , т.к. вектор
, т.к. вектор 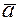 коллинеарен
коллинеарен 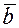 , тогда
, тогда 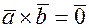 , согласно предыдущей теореме, выполняются равенства
, согласно предыдущей теореме, выполняются равенства 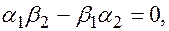

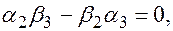
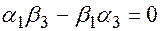 , получаем пропорцию
, получаем пропорцию 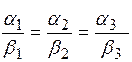 .
.
Дата добавления: 2015-08-26; просмотров: 880;
