Лекция 6. Векторное произведение векторов, смешанное произведение векторов, основные свойства

Векторное произведение векторов, смешанное произведение векторов, основные свойства. Условия ортогональности, коллинеарности, компланарности векторов.

Цель: Изучить векторное и смешанное произведение векторов, их свойства, методы вычисления, условия ортогональности, компланарности и коллинеарности векторов.

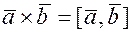Определение. Векторным произведением двух векторов , обозначают называется вектор 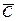удовлетворяющий трем условиям:

1) Модуль вектора равен площади параллелограмма, построенного на этих векторах

(6.1)

2) Вектор ортогонален перемножаемым векторам: 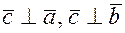т.е. ортогонален плоскости построенного на этих векторах параллелограмма

3) 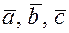составляют правую тройку векторов (рис.6.1).

Рис. 6.1