Свойства скалярного произведения
1) 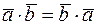 (коммутативность).
(коммутативность).
Непосредственно следует из коммутативности произведения чисел;
2) 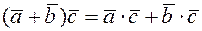 (дистрибутивность).
(дистрибутивность).
Для доказательства этого свойства воспользуемся линейным свойством проекции и формулой, связывающей скалярное произведение и проекцию. Поскольку 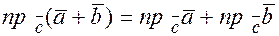 и
и 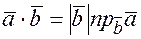 , тогда
, тогда 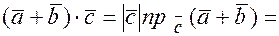
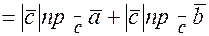 =
= 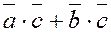 ;
;
2) Скалярный квадрат вектора равен квадрату модуля этого вектора:
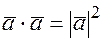 (5.5)
(5.5)
Выполняется для любого вектора 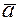 , следует из определения, поскольку угол
, следует из определения, поскольку угол 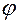 между вектором
между вектором 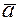 и
и 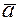 равен нулю, тогда
равен нулю, тогда 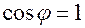 ;
;
4) Скалярный множитель можно выносить за знак скалярного произведения
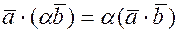
где 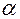 - произвольное действительное число.
- произвольное действительное число.
Доказывается по аналогии со свойством 2. Поскольку 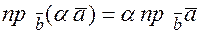 и
и 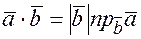 , тогда
, тогда 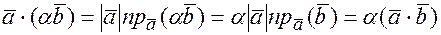 ;
;
5) Скалярное произведение равно нулю тогда и только тогда, когда их скалярное произведение равно нулю.
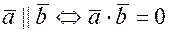 (5.6)
(5.6)
Доказательство. Докажем, что если векторы ортогональны, то их скалярное произведение равно нулю. Действительно, если 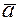 и
и 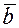 ортогональны, следовательно,
ортогональны, следовательно, 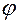 - угол между векторами
- угол между векторами  равен
равен 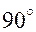 , тогда
, тогда 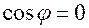 , тогда из определения следует, что
, тогда из определения следует, что 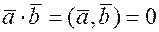 .
.
Докажем теперь, что если скалярное произведение векторов  равно нулю, то они ортогональны. Пусть оба вектора ненулевые, (т.к. в противоположном случае доказательство тривиально, поскольку нулевой вектор не имеет определенного направления и его можно считать ортогональным любому вектору). Тогда
равно нулю, то они ортогональны. Пусть оба вектора ненулевые, (т.к. в противоположном случае доказательство тривиально, поскольку нулевой вектор не имеет определенного направления и его можно считать ортогональным любому вектору). Тогда 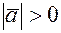 и
и 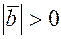 , поэтому
, поэтому 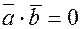 только в том случае, если
только в том случае, если 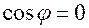 , т.е. векторы
, т.е. векторы  должны быть ортогональны.
должны быть ортогональны.
6) векторы ортонормированного базиса декартовой прямоугольной системы координат 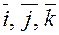 удовлетворяют соотношениям:
удовлетворяют соотношениям:
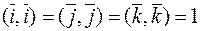 ,
, 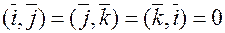 т.к. векторы попарно ортогональны
т.к. векторы попарно ортогональны 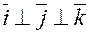 .
.
Если базисные векторы 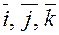 ортогональны, то для каждого вектора
ортогональны, то для каждого вектора 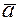 координаты в данном базисе будут равны:
координаты в данном базисе будут равны: 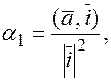
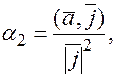
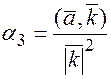 , поскольку
, поскольку 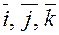 – ортонормированный базис, тогда
– ортонормированный базис, тогда 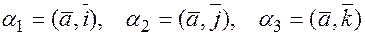 .
.
Геометрический смысл скалярного произведения: с помощью скалярного произведения можно вычислить проекцию вектора 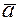 на вектор
на вектор 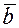 , и косинус угла между векторами:
, и косинус угла между векторами:

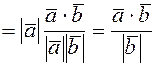 (5.7)
(5.7)
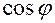
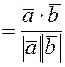 (5.8)
(5.8)
Теорема. Если базис ортонормированный и 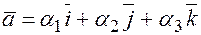 ,
, 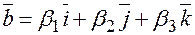 , то
, то
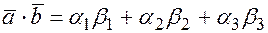 (5.9)
(5.9)
где 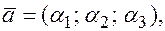
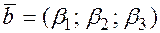 – координаты векторов в ортонормированном базисе.
– координаты векторов в ортонормированном базисе.
Доказательство. Поскольку 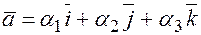 и
и 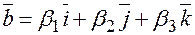 , тогда найдем скалярное произведение векторов используя свойства дистрибутивности и ассоциативности:
, тогда найдем скалярное произведение векторов используя свойства дистрибутивности и ассоциативности:
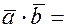
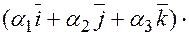
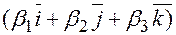 =
=
= 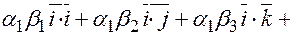
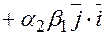
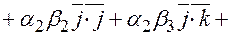
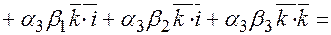
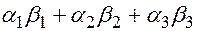 .
.
Следствие. Необходимым и достаточным условием ортогональности векторов 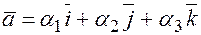 и
и 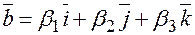 является условие
является условие 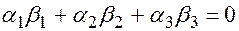 .
.
Следствие. Длина (модуль) вектора 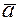 равна
равна 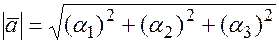 .
.
Следствие. 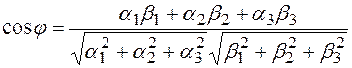 , где
, где 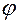 - угол между векторами
- угол между векторами  .
.
Следствие. Если 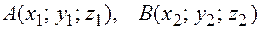 , тогда:
, тогда:
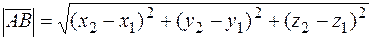 .
.
Дата добавления: 2015-08-26; просмотров: 1437;
