Свойства проекции

1) Проекция суммы векторов равна сумме проекций составляющих 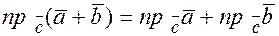(рис. 5.2).

Рис. 5.2

2) Проекция произведения вектора на число равна произведению числа на проекцию данного вектора 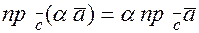(рис. 5.3).

Рис 5.3.

Теорема. Чтобы найти компоненты вектора, нужно из координат его конца вычесть координаты его начала, т.е.

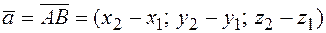, где 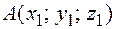, 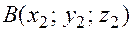(рис. 5.4).

Рис. 5.4

Найдем координаты точки 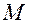, которая делит 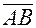в отношении 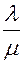( 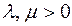). Отношение 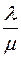, в котором произвольная точка 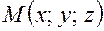делит отрезок 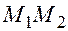(Рис. 5.5) удовлетворяет равенству .

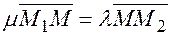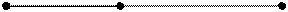
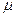
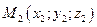
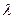
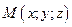
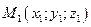
Рис.5.5.

Пусть 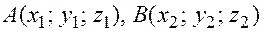, а 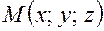, тогда разложим обе части равенства по базису 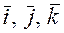, тогда , ,

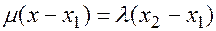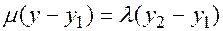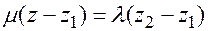
т.к. 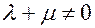, следовательно

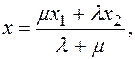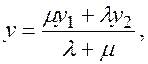
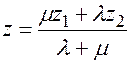. (5.1)

Когда 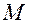делит отрезок пополам, имеем:

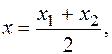
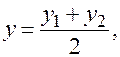
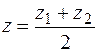. (5.2)