Теорема.

1. Если хотя бы один из векторов 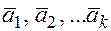, является нулевым, то эти векторы линейно зависимы.

2. Любые два коллинеарных вектора линейно зависимы, и наоборот, два линейно зависимых вектора коллинеарные.

3. Каждые три компланарных вектора линейно зависимы, и наоборот, три линейно зависимых вектора компланарны.

4. Каждые четыре вектора линейно зависимы.

Доказательство. (Приведем доказательство 1–го и 2–го утверждений теоремы, остальные доказываются аналогично).

1. Поскольку среди векторов есть нулевой, значит, в их линейной комбинации перед нулевым вектором может стоять любой ненулевой элемент, а перед остальными векторами будут стоять нулевые элементы, это и означает линейную зависимость векторов.

2. Докажем, что если два вектора 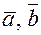коллинеарны, то они линейно зависимы. Если хотя бы один из векторов 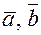нулевой, то они линейно зависимы в силу предыдущего утверждения теоремы.

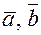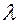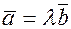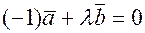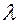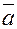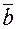Если оба вектора ненулевые, то из свойства коллинеарности векторов следует, что существует действительное число такое, что или , поскольку и отличны от нуля и линейно зависимы.

Докажем теперь, что два линейно зависимых вектора ­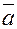- и 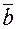коллинеарны. Поскольку 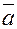и 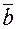линейно зависимы, следовательно, по определению, существуют действительные числа 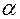и 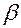, хотя бы одно из них отлично от нуля, такие, что 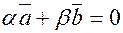, пусть 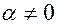, тогда 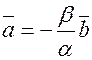, пусть 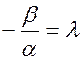, имеем 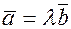, согласно свойству произведения вектора на число, это и означает коллинеарность векторов 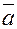и .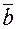

Базис.

Определение.Базисом на прямой называется любой ненулевой вектор лежащий на этой прямой или коллинеарный с ней.

Определение. Базисом на плоскости называются два неколлинеарных вектора лежащих на этой плоскости или параллельных ей, взятые в определенном порядке.

Определение.Базисом в пространстве называют три некомпланарных вектора, взятых в определенном порядке.

Определение. Говорят, что три линейно независимых вектора 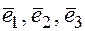образуют базис в пространстве 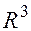, если каждый вектор этого пространства можно представить как линейную комбинацию этих векторов, т.е. . Числа называются координатами вектора 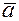в базисе 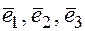и вектор 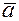обычно записывают как .

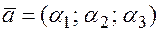Выражение называется линейной комбинацией вектора или разложением по базису.

Запись 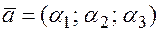называется координатной формой записи вектора.

Равные векторы в одном базисе имеют равные компоненты.

При умножении вектора на число каждая его координата умножается на это число, т.е. если 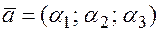, то = .

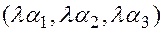При сложении двух векторов их координаты, стоящие перед соответствующими базисными векторами, складываются, т.е. = .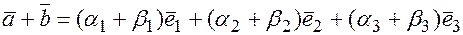

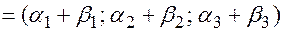Утверждение. Любые три некомпланарных вектора, взятые в определенном порядке, образуют базис пространства.

Любые два неколлинеарных вектора на плоскости, взятые в определенном порядке, образуют базис на этой плоскости.

Любой ненулевой вектор, лежащий на прямой, образует базис на этой прямой.