Свойства линейной комбинации
1. Если 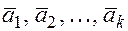 – параллельны, то каждая их линейная комбинация параллельна им.
– параллельны, то каждая их линейная комбинация параллельна им.
2. Если 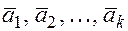 – компланарны, то каждая их линейная комбинация компланарна с ними.
– компланарны, то каждая их линейная комбинация компланарна с ними.
Определение. Пусть дана линейная комбинация 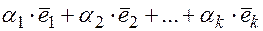 , если
, если 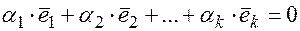 только при условии, что
только при условии, что 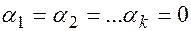 , тогда линейная комбинация векторов называется тривиальной линейной комбинацией, если
, тогда линейная комбинация векторов называется тривиальной линейной комбинацией, если 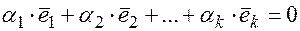 , и существует хотя бы один
, и существует хотя бы один 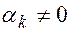 , то
, то 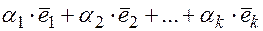 – нетривиальная линейная комбинация.
– нетривиальная линейная комбинация.
Определение. Если существуют такие 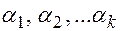 , что
, что 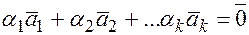 – нетривиальная линейная комбинация, то говорят, что
– нетривиальная линейная комбинация, то говорят, что 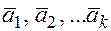 - линейно зависимы. В противном случае, т.е. если
- линейно зависимы. В противном случае, т.е. если 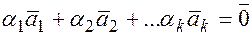 – тривиальная линейная комбинация, то
– тривиальная линейная комбинация, то 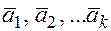 – линейно независимы.
– линейно независимы.
Теорема. Векторы 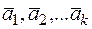 линейно зависимы тогда и только тогда, когда один из них является линейной комбинацией остальных.
линейно зависимы тогда и только тогда, когда один из них является линейной комбинацией остальных.
Доказательство. Необходимость. Докажем, что если векторы 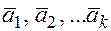 линейно зависимы, то один из них является линейной комбинацией остальных. Поскольку векторы линейно зависимы, то, согласно определению, существует
линейно зависимы, то один из них является линейной комбинацией остальных. Поскольку векторы линейно зависимы, то, согласно определению, существует 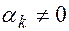 , при котором
, при котором 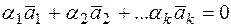 .
.
Пусть 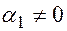 , тогда
, тогда 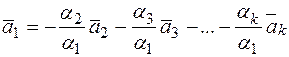 . Т.е. вектор
. Т.е. вектор 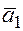 является линейной комбинацией остальных.
является линейной комбинацией остальных.
Достаточность. Докажем, что если один из векторов 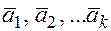 является линейной комбинацией остальных, то векторы линейно зависимы. Пусть
является линейной комбинацией остальных, то векторы линейно зависимы. Пусть 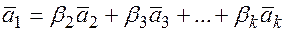 – линейная комбинация остальных векторов, тогда
– линейная комбинация остальных векторов, тогда 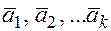 – линейно зависимы, поскольку
– линейно зависимы, поскольку 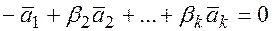 при том, что
при том, что 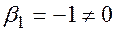 .
.
Дата добавления: 2015-08-26; просмотров: 1919;
