Векторная алгебра. Понятие вектора, координаты, модуль вектора. Линейные операции над векторами. Базис

Цель: Изучить понятие вектора, равенства векторов, как определяются координаты вектора его модуль, линейные операции над векторами и их свойства, понятие базиса.

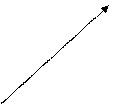
Определение. Направленный отрезок (упорядочивающий пару точек) будем называть вектором и обозначать 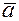, , 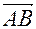где точку 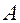называют началом вектора, а 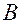– его концом (рис.4.1).

Необходимо знать, что в печатных изданиях часто векторные величины и векторы обозначают жирным шрифтом, без стрелки

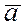
Рис. 4.1

Расстояние между началом и концом вектора называется его длиной, модулем или абсолютной величиной вектора и обозначают , .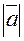

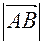Векторы называются коллинеарными, если существует прямая, которой эти векторы параллельны, пишут 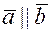. Коллинеарные векторы могут быть сонаправленными (направлены в одну сторону), и противоположно направленными. Обозначается соответственно , .

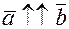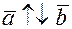Векторы называются компланарными, если существует плоскость, которой они параллельны.

Нулевой вектор считается коллинеарным любому вектору т.к. не имеет направления.

Свойство.Если вектор 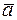коллинеарен ненулевому вектору 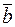, то существует действительное число 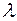такое, что .

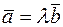Определение. Два вектора 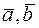считаются равными, если выполнено три условия: 1) их модули равны, 2) они параллельны, 3) направлены в одну сторону.

О равенстве векторов стоит поговорить отдельно, т.к. оно существенно отличается от равенства чисел. Два равных числа могут рассматриваться как одно и тоже. С векторами все иначе.

Из курса физики известно, что сила может быть изображена вектором. Но, силы изображаемые равными направленными отрезками производят, вообще говоря различные действия. Так сила действующая на упругое тело изображается направленным отрезком, который не может быть никуда перенесен из данной точки. Т.е. он характеризуется направлением и точкой приложения и называется приложенным вектором.

Сила действуещая на абсолютно твердое тело, изображается скользящим вектором, который может быть перенесен не в любую точку пространства, а лишь вдоль прямой на которой он лежит.

Все остальные равные вектора (множество направленных отрезков, равных данному) называются свободными векторами, с которыми мы и будем работать.