Понятие многочлена, корни многочленов, кратность корня, основные теоремы алгебры, следствия из теорем.
3.Возведение в степень.
Для возведения комплексного числа в целую положительную степень 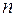 применяют формулу Муавра:
применяют формулу Муавра:
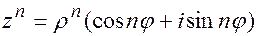 (3.1)
(3.1)
Данная формула является следствием формулы (2.14).
Пример. Возвести комплексное число в степень:
1) 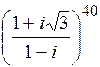 .
.
Решение. 1. Пусть 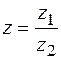 , тогда для комплексного числа в числителе и знаменателе найдем модуль и аргумент и перепишем
, тогда для комплексного числа в числителе и знаменателе найдем модуль и аргумент и перепишем 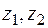 в показательной форме, имеем
в показательной форме, имеем 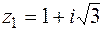 , значит
, значит 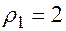 ,а
,а 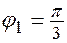 ,
, 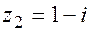 ,
, 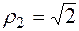 ,
, 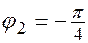 , тогда получим
, тогда получим
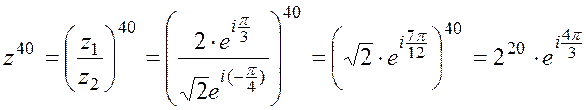
4.Извлечение корня порядка 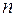 .
.
Определение. Корнем  -й степени из комплексного числа
-й степени из комплексного числа 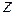 называется комплексное число
называется комплексное число 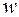 , такое что
, такое что 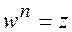 , где
, где  - натуральное число. Обычно используется обозначение
- натуральное число. Обычно используется обозначение 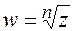 .
.
Корень  -й степени из комплексного числа имеет
-й степени из комплексного числа имеет  различных значений, которые находятся по формуле Муавра-Лапласа:
различных значений, которые находятся по формуле Муавра-Лапласа:
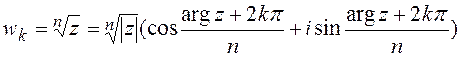 (3.2)
(3.2)
Или через показательную форму
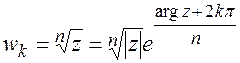 (3.3)
(3.3)
Где 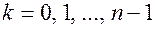 .
.
Точки, соответствующие 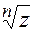 являются вершинами правильного
являются вершинами правильного  – угольника, вписанного в окружность с центром в начале координат и радиусом
– угольника, вписанного в окружность с центром в начале координат и радиусом 
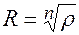 .
.
Способ построения для 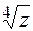 (рис.3.1):
(рис.3.1):
1) Из начала координат описываем окружность радиуса 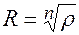 .
.
2) Если 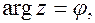 то из начала координат проводим луч под углом
то из начала координат проводим луч под углом 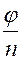 к положительному направлению
к положительному направлению 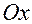 . Пересечение луча с окружностью дает точку
. Пересечение луча с окружностью дает точку 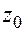 .
.
3) Вписываем в окружность правильный  – угольник, одна из вершин которого найденная точка
– угольник, одна из вершин которого найденная точка 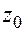 . Точки пересечения
. Точки пересечения  – угольника и окружности есть решения
– угольника и окружности есть решения 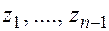 .
.
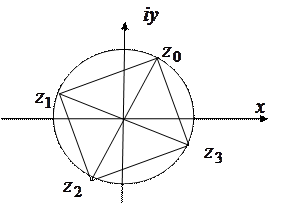 |
Рис. 2.2
Пример. Найдем все значения 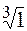 .
.
Решение. Тригонометрической формой числа 1 является: 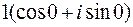 .
.
Значениями 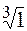 являются числа:
являются числа: 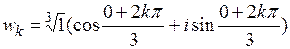 , различными будут лишь корни при следующих значениях
, различными будут лишь корни при следующих значениях 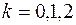 ,
, 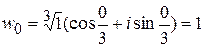 ;
; 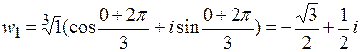 ;
; 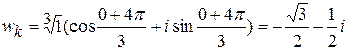 .
.
Полученные значения являются вершинами правильного треугольника вписанного в окружность радиуса 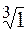 .
.
Пример. Корни 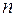 -ой степени из единицы
-ой степени из единицы 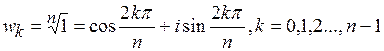 есть вершины правильного n-угольника, вписанного в единичный круг.
есть вершины правильного n-угольника, вписанного в единичный круг.
Определение. Многочленом одной переменной называется функция 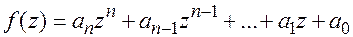 , где
, где 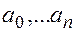 - действительные или комплексные коэффициенты, а
- действительные или комплексные коэффициенты, а 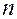 - целое неотрицательное число. Если
- целое неотрицательное число. Если 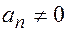 ,
, 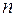 называют степенью многочлена и обозначают
называют степенью многочлена и обозначают 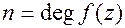 , а
, а 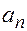 - старшим коэффициентом. Многочлен
- старшим коэффициентом. Многочлен 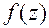 называется нулевым, если все его коэффициенты равны нулю. Коэффициент
называется нулевым, если все его коэффициенты равны нулю. Коэффициент 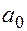 при
при 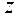 в нулевой степени называют постоянным или свободным членом.
в нулевой степени называют постоянным или свободным членом.
Многочлены степени 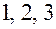 называются соответственно линейными, квадратичными (или квадратными), кубичными и т.д. В дальнейшем рассматриваются только действительные коэффициенты
называются соответственно линейными, квадратичными (или квадратными), кубичными и т.д. В дальнейшем рассматриваются только действительные коэффициенты 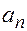 .
.
Определение. Корнем многочлена 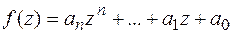 называется такое
называется такое 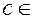
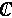 , при котором
, при котором 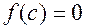 .
.
Основная теорема алгебры. Всякий многочлен положительной степени имеет, по крайней мере, один корень действительный или комплексный.
Деление многочленов.Из курса элементарной алгебры известен метод деления уголком для целых чисел, аналогичный алгоритм имеет место и для многочленов.
Пусть даны два многочлена: 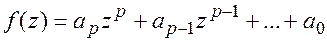 и
и 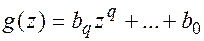 , где
, где 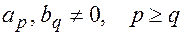 и, тогда многочлену
и, тогда многочлену 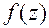 сопоставляется одна и только одна пара многочленов
сопоставляется одна и только одна пара многочленов 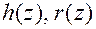 , для которых
, для которых 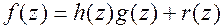 ,
, 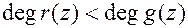 ,
, 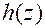 называют частным деления, а
называют частным деления, а 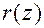 - остатком.
- остатком.
Если 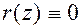 , тогда говорят, что
, тогда говорят, что 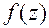 делится на
делится на 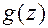 .
.
Если многочлены имеют действительные коэффициенты, то 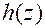 и
и 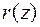 также имеют действительные коэффициенты.
также имеют действительные коэффициенты.
Пример. Проверить, делится ли многочлен 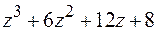 на
на 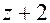 .
.
Решение. Разделим многочлены столбиком, т.е.
_ 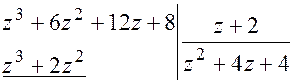
_ 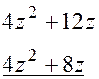
_ 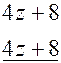
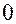 :
:
Итак,многочлен 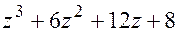 делится на
делится на 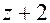 и может быть представлен в виде
и может быть представлен в виде 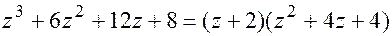 .
.
Теорема Безу. Число 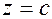 является корнем многочлена
является корнем многочлена 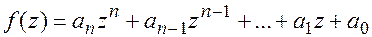 тогда и только тогда, когда
тогда и только тогда, когда 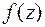 делится на линейный многочлен (
делится на линейный многочлен ( 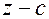 ).
).
Доказательство. В результате деления 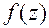 на (
на ( 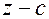 ) имеем
) имеем 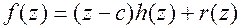 . Степень
. Степень 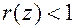 , значит
, значит 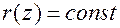 тогда подставим
тогда подставим 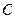 в
в 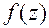 , получим
, получим 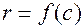 , следовательно
, следовательно 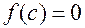 и
и 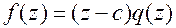 .
.
Теорема. При делении 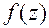 на
на 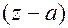 , остаток
, остаток 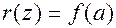 , т.е.
, т.е. 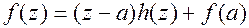 .
.
Пример. Проверить, делится ли многочлен 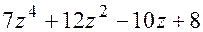 на
на 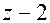 .
.
Решение. Разделим многочлены столбиком, т.е.
_ 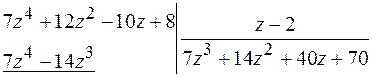
_ 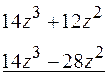
_ 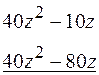
_ 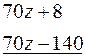
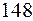 ;
;
степень остатка меньше степени делителя, останавливаем деление.
Итак,многочлен 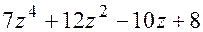 не делится на
не делится на 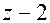 и может быть представлен в виде
и может быть представлен в виде 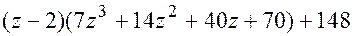 .
.
Проверить, правильно ли выполнено деление можно, используя предыдущую теорему, согласно которой 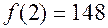 , действительно,
, действительно, 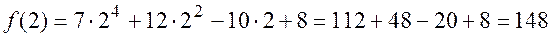 , значит деление выполнено правильно.
, значит деление выполнено правильно.
Определение. Число 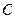 называется
называется 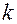 – кратным корнем многочлена
– кратным корнем многочлена 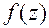 , если
, если 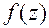 делится на
делится на 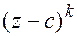 , но не делится на
, но не делится на 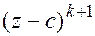 . Корень кратности
. Корень кратности 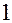 называют простым корнем.
называют простым корнем.
Теорема. Если 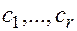 - корни многочлена
- корни многочлена 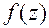 степени
степени 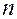 – кратности
– кратности 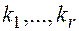 соответственно и
соответственно и 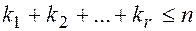 , тогда
, тогда 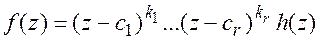 , где
, где 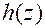 – многочлен степени (
– многочлен степени ( 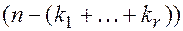 такой, что
такой, что 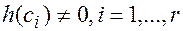 .
.
Доказательство данной теоремы следует из теоремы Безу.
Правило определения кратности корня
Пусть 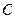 – корень кратности
– корень кратности 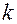 многочлена
многочлена 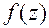 степени
степени 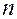 , тогда
, тогда
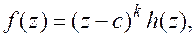
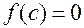 , где
, где 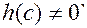 и
и 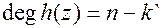
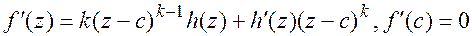 , где
, где 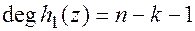 , продолжая вычислять производные на
, продолжая вычислять производные на 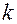 – ом шаге получим,
– ом шаге получим,
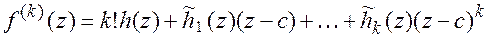 , т.к.
, т.к. 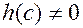 , следовательно,
, следовательно, 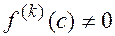 , тогда можно предложить следующее правило для вычисления кратности корня многочлена.
, тогда можно предложить следующее правило для вычисления кратности корня многочлена.
Для того чтобы определить кратность корня 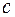 многочлена
многочлена 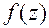 , вычисляем значения производных
, вычисляем значения производных 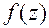 в точке
в точке 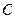 и как только
и как только 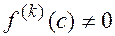 , тогда
, тогда 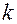 - кратность корня.
- кратность корня.
Дата добавления: 2015-08-26; просмотров: 2088;
