Геометрический смысл комплексного числа

Комплексное число 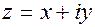изображается в плоскости 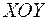точкой 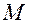с координатами 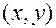либо вектором, начало которого находится в точке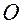 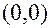, а конец в точке 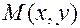(рис. 1.3).

Длина 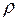вектора 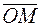называется модулем комплексного числа и обозначается

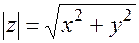(2.3)

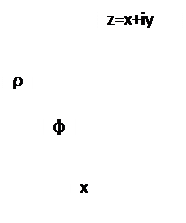
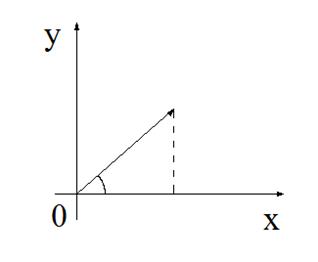
Рис. 2.1

Угол 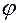, образованный положительным направлением оси ОХ и вектором 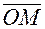, называется аргументом комплексного числа и обозначается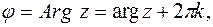 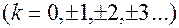, где 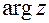– главное значение аргумента, 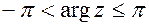. Главное значение аргумента комплексного числа может быть найдено с помощью формулы:

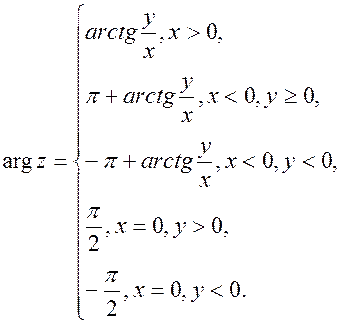(2.5)

Если в алгебраической форме записи комплексного числа вместо декартовых координат точки подставить их полярное представление (1.4), то получим тригонометрическое представление комплексного числа.

Определение. Каждое комплексное число, отличное от нуля, можно записать в тригонометрической форме

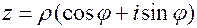(2.6)

где .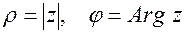

С помощью формулы Эйлера:

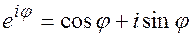(2.7)

каждое комплексное число может быть записано в показательной форме

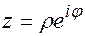. (2.8)

Число 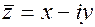называется сопряженным комплексному числу .

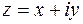Выполняются следующие равенства: ; ;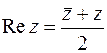

;

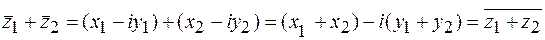Аналогично доказывается, что ; ; .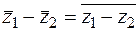

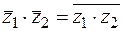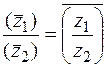Важно знать, что 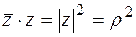(2.9)