Системы координат. 1. Декартова система координат.

1. Декартова система координат.

Рис.1.1

Возьмем в пространстве произвольную точку 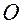и рассмотрим некоторую точку 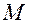. Соединив эти точки мы получим вектор, который называется радиус-вектором точки 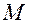по отношению к точке 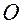. Если в пространстве выбрать какой-либо базис (рис 1.1), то точке 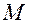можно поставить в соответствие упорядоченную тройку чисел – компоненты ее радиус-вектора.

Определение: Декартовой системой координат в пространстве называется совокупность точки и базиса. Итак, рассматриваем три взаимно ортогональные оси в трехмерном пространстве, исходящие из общей точки 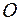(начала координат и образующие правую тройку).

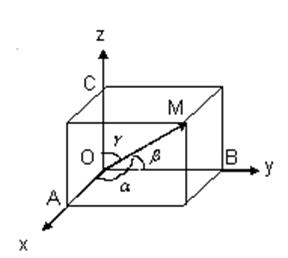
Рис.1.2.

Оси 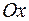, , 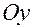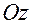называются осями координат: абсцисса, ордината и аппликата. Плоскости 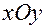, , 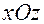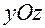называются координатными плоскостями, которые делят все пространство на октаны. Мы рассматриваем радиус-вектор точки .

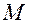Определение: Под декартовыми прямоугольными координатам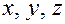и точки 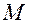понимаются проекции ее радиус-вектора 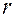на соответствующие оси координат, т.е. 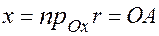, , 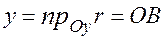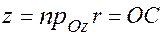(рис.1.2.). Для краткости их просто называют прямоугольными координатами.

Легко видеть, что при заданной системе координат координаты точки определены однозначно. И наоборот, каждая упорядоченная тройка чисел определяет единственным образом точку в пространстве.

Радиус-вектор является диагональю параллелепипеда. Поэтому

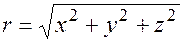(1.1)

Если обозначить через 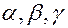углы, образованные радиус-вектором с координатными осями (рис.1.2.), то будем иметь:

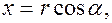
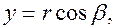
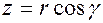(1.2)

Эти косинусы называются направляющими косинусами радиус-вектора точки 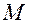. Из (2), учитывая (1), получаем важное соотношение:

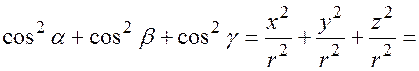
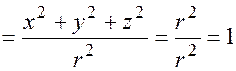(1.3)

т.е. сумма квадратов направляющих косинусов радиус-вектора точки пространства равна единице.

Из формулы (2) следует, что координата точки 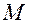положительна, если радиус-вектор этой точки образует с осью острый угол, и отрицательна, если этот угол тупой.

Измерения 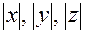параллелепипеда равны расстояниям точки 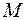соответственно от координатных плоскостей , , .

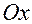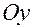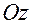Определение: Декартовые прямоугольные координаты точки 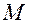пространства представляют собой расстояния от этой точки до координаты плоскостей, взятые с надлежащим знаком.

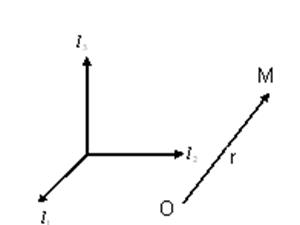
Кроме прямоугольной декартовой системы координат используют полярную систему координат. Эта система определена на плоскости, если существует точка 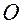, называемая полюсом и исходящий из этого полюса луч 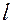, который называется полярной осью.

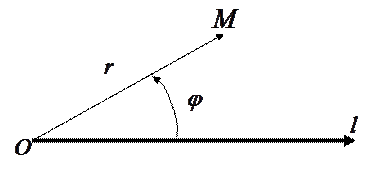
Рис.1.3.

В данной системе положение точки фиксируется двумя числами: радиус-вектором точки 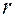и углом 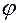между полярной осью и вектором 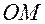, т.е.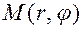

Угол 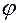называется полярным, отсчитывается от полярной оси в направлении против часовой стрелки. У плюса точки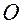 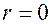, а угол не определен. У всех остальных точек 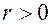и 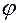изменяется в пределах от 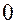до 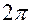, измеряется в радианах.

Если мы поместим полярную систему координат полюсом в начало прямоугольной декартовой системы координат, то декартовы координаты будут выражаться через полярные по формулам:

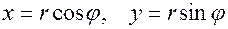(1.4)

Полярные координаты через декартовые выражаются соотношениями:

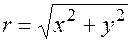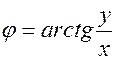, (1.5)