И . Системы координат: декартовая, полярная.

КОНСПЕКТЫ ЛЕКЦИЙ

Аналитическая геометрия и алгебра

Самолето и вертолето строение

г. Владивосток

Лекция 1

Конечные суммы и их свойства. Вычисление определителя

и . Системы координат: декартовая, полярная.

Цель: Изучить понятие конечной суммы и ее свойства, понятие определителя и простейшие методы его вычисления. Знать декартовую и полярную системы координат.

В математике часто рассматривают суммы большого числа слагаемых которые имеют один и тот же вид, но различаются индексами. Для них используют символ суммы 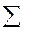(от латинского слова 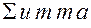). Под символом суммы ставится «индекс суммирования» (любая буква) и значение от которого наш индекс изменяется (некоторое целое число) сверху над символом ставится значение, до которого данный символ изменяется – это пределы суммирования. После символа суммы ставится суммируемое выражение.

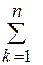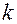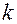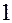Определение.Символ , после которого стоит некоторое выражение, содержащее индекс , обозначает сумму этих выражений для всех значений индекса от до 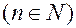и называется конечной суммой и записывается 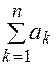или .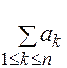

Здесь символ 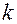- индекс суммирования, интервал 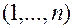- интервал суммирования, 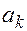- суммируемое выражение.

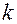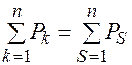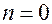Очевидно, что вместо может быть взята любая другая буква, т.е. .Если или 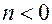, то значение суммы равно нулю.

Примеры:

1) ;

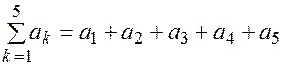2)

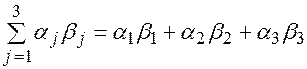
Замечание. Иногда вместо 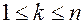пишут 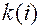, тогда символ 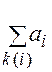означает сумму всех таких 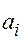, что целое число 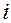удовлетворяет условиям 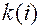. Если таких целых 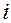нет, сумма считается равной 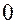. Наконец, если 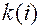включает два или больше условий, это означает, что все условия должны выполняться одновременно.