Теорема. При плоско-параллельном движении твердого тела скорость любой его точки равна векторной сумме скорости полюса и скорости во вращательном движении вокруг полюса.

Доказательство. Пусть полюс О движется со скоростью υ₀, а плоская фигура вращается вокруг полюса с угловой скоростью ω (рис. 71). Требуется определить скорость произвольной точки М этой фигуры. Так как переносным здесь является поступательное движение вместе с полюсом О, то переносные скорости всех точек плоской фигуры будут одинаковыми, равными скорости полюса:

υ_Me= υ₀

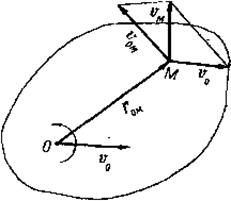
Относительным движением является вращательное движение вокруг полюса. Поэтому, обозначая радиус-вектор точки М относитель­но полюса О через r_OM , согласно формуле Эйлера, для относительной скорости точки М получим

υ_Mr= ω x r_OM.

Относительную скорость точки при плоско-парал­лельном движении тела обозначают двойным индексом, т. е. υ_Mr = υ_OM. Первый индекс указывает полюс О, вокруг которого происходит вращение, а второй — обозначает рассматриваемую точку М. Следовательно,

υ_Mr= υ_OM= ω x r_OM

По теореме о сложении скоростей получим

υ_a=υ_e+υ_r.

Следовательно,

υ_M=υ_O+υ_OM.

Или

υ_M=υ_O+ω x r_OM