Кинематические уравнения плоско-параллельного движения

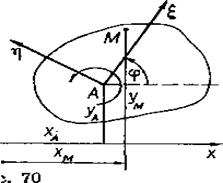
Допустим, что плоская фигура движется в неподвиж­ной плоскости Оху. Выбрав, например, точку А плоской фигуры за полюс, неизменно свяжем с этой фигурой подвижную систему координат Аξη с началом в полюсе А (рис. 70). Для определения положения подвижной системы координат Аξη относительно не­подвижной нужно знать координаты точки А (т. е. х_A и у_A), а также угол поворота φ вокруг полюса (т. е. угол, образованный осью Аξη с осью Ох). Следователь­но, кинематические уравнения плоско-параллельного движения твердого тела имеют вид

x_A= x_A(t) . y_A = y_A (t). φ = φ (t),

где x_A(t) y_A (t), φ (t)— конечные, однозначные, непрерывные и дифференцируемые функции времени.

Пользуясь формулами преобразования координат, можно полу­чить уравнения движения любой точки М плоской фигуры

x = x_A + ξcos φ —ηsin φ,

y = y_A + ξsin φ + ηcos φ -