Сложение поступательных движений твердого тела

Теорема. В результате сложения мгновенных поступательных движений твердого тела получается результирующее мгновенно поступательное движение.

Доказательство. Пусть твердое тело одновременно участвует в двух мгновенных поступательных движениях, из которых одно является относительным со скоростью υ₁ а второе — переносным со скоростью υ₂.

По теореме о параллелограмме скоростей имеем для любой точки твердого тела

υ_а = υ_r + υ_e = υ₁+ υ₂,

А так как и относительное, и переносное движения твердого тела являются мгновенно поступательными, то относительные, переносные и, следовательно, согласно формуле (II.98), абсолютные скорости всех точек тела соответственно между собой равны в каждый момент времени, т.е. абсолютное движение тела также является мгновенно поступательным. Теорема доказана.

Очевидно, что данная теорема применима к сложному движению твердого тела, состоящему из трех и более мгновенно поступательных движении; тогда в общем случае

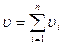
Заметим, что мгновенно поступательное твердого тела отличается от поступательного тем, что во втором случае в каждый момент времени равны между собой скорости и ускорения всех точек тела, между тем, как в первом случае в данный момент времени равны между собой только скорости всех точек тела.