Векторная диаграмма. Сложение колебаний.

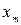Решение ряда задач теории колебаний значительно облегчается и становится более наглядным, если изображать колебания графически, используя метод векторных диаграмм. Выберем некоторую ось х . Из точки 0 на оси отложим вектор длины , образующий вначале с осью угол (рис.2.14.1). Если привести этот вектор во вращение с угловой скоростью 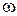, то проекция конца вектора на ось х будет изменяться с течением времени по закону

.

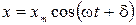Следовательно, проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, который образует вектор с осью в начальный момент времени. Угол, образованный вектором с осью в данный момент времени определяет фазу колебания в этот момент - .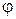

Из сказанного следует, что гармоническое колебание можно представить с помощью вектора, длина которого равна амплитуде колебания, а направление его образует с некоторой осью угол, равный фазе колебания. В этом и состоит суть метода векторных диаграмм.

Сложение колебаний одинакового направления.

Рассмотрим сложение двух гармонических колебаний, направления которых параллельны:

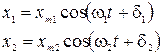. ( 2.14.1 )

Результирующее смещение х будет суммо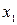й и 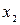. Это будет колебание с амплитудой .

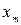Воспользуемся методом векторных диаграмм (рис.2.14.2). На рисунке 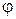, 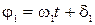и 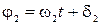- фазы результирующего и складываемых колебаний соответственно. Легко видеть, что 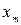можно найти сложением векторов и 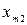. Однако, если частоты складываемых колебаний различны, то результирующая амплитуда меняется с течением времени по величине и вектор вращается с непостоянной скоростью, т.е. колебание не будет гармоническим, а будет представлять некоторый сложный колебательный процесс. Чтобы результирующее колебание было гармоническим, частоты складываемых колебаний должны быть одинаковы

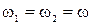
и результирующее колебание происходит с той же частотой

.

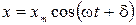Из построения видно, что

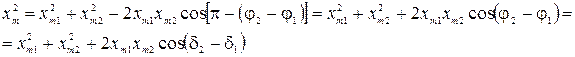(2.14.2)

Проанализируем выражение (2.14.2) для амплитуды результирующего колебания. Если разность фаз складываемых колебаний равна нулю (колебания синфазны), амплитуда равна сумме амплитуд складываемых колебаний, т.е. имеет максимальное из возможных значение 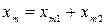. Если разность фаз составляет (колебания находятся в противофазе), то результирующая амплитуда равна разности амплитуд, т.е. имеет минимальное из всех возможных значение .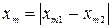

Сложение взаимно перпендикулярных колебаний.

Пусть частица совершает два гармонических колебания с одной и той же частотой: одно вдоль направления, которое обозначим х, другое – в перпендикулярном направлении y . В этом случае частица будет двигаться по некоторой, в общем случае, криволинейной траектории, форма которой зависит от разности фаз колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза одного колебания была равна нулю:

. ( 2.14.3 )

Чтобы получить уравнение траектории частицы, нужно из (2.14.3) исключить t . Из первого уравнения 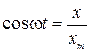, а. значит, . Второе уравнение перепишем

или

.

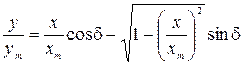Перенеся первое слагаемое из правой части уравнения в левую, возведя полученное уравнение в квадрат и проведя преобразования, получим

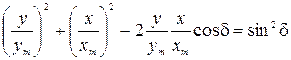. ( 2.14.4 )

Это уравнение представляет собой уравнение эллипса, оси которого повернуты относительно осей х и y на некоторый угол. Но в некоторых частных случаях получают более простые результаты.

1. Разность фаз равна нулю. Тогда из (2.14.4) получим

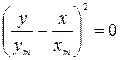или 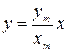. ( 2.14.5 )

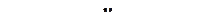Это уравнение прямой (рис.2.14.3). Таким образом, частица совершает колебания вдоль этой прямой с частотой 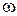и амплитудой, равной .

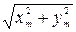2. Разность фаз 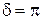. В этом случае из (2.14.4) следует, что результирующее движение представляет собой гармоническое колебание вдоль прямой

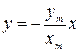. ( 2.14.6 )

3. При 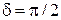уравнение (2.14.4) переходит в

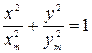. ( 2.14.7 )

Это уравнение эллипса, оси которого совпадают с координатными осями (рис.2.14.4). При равенстве амплитуд по обеим осям эллипс вырождается в окружность.

Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу.