Лекция 2.11.

В 1831 г. английский физик М.Фарадей совершил одно из наиболее фундаментальных открытий в электродинамике – открытие явления электромагнитной индукции. Суть его состоит в том, что при любом перемещении проводящего контура в магнитном поле в контуре возникает электрический ток. Ток возникает также и при изменении величины и направления индукции магнитного поля, в котором находится этот контур. Такой ток называется индукционным.

Э.д.с. индукции. Закон Фарадея. Правило Ленца.

Появление индукционного тока в контуре означает, что при всех вышеперечисленных манипуляциях в контуре возникает электродвижущая сила. Заметим, что все приведенные примеры можно формально объединить, указав следующий факт: во всех случаях через поверхность, опирающуюся на контур, меняется магнитный поток – поток вектора ( ).

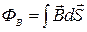Единицей измерения магнитного потока в системе СИ является вебер (Вб).

Таким образом, закон Фарадея гласит: В замкнутом проводящем контуре при изменении магнитного потока через поверхность, ограниченную этим контуром, возникает электрический (индукционный) ток.

Направление индукционного тока определяется правилом Ленца: индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, вызвавшего этот индукционный ток. Рассмотрим пример. Возьмем контур, как показано на рис. 2.11.1 с подвижной перемычкой. Приведем перемычку в движение, как показано на рисунке. Тогда магнитный поток через поверхность, ограниченную контуром, будет возрастать. Чтобы противодействовать этому увеличению, индукционный ток будет течь, как показано на рисунке.

Закон электромагнитной индукции можно представить математически. Э.д.с. индукции можно определить:

Є 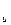= 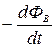. ( 2.11.1 )

Знак минус в этом уравнении связан с определенным правилом знаков: знак магнитного потока связан с выбором нормали к поверхности, ограниченной рассматриваемым контуром, а знак э.д.с. индукции – с выбором положительного обхода по контуру.

В качестве примера найдем э.д.с. индукции, возникающую в контуре, изображенном на рис. 2.11.1. Пусть магнитное поле будет однородным, а нормаль к площадке, ограниченной контуром, направлена от нас, длина перемычки l .Тогда магнитный поток, пронизывающий площадку равен 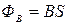, а его изменение 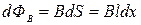, где dx – перемещение перемычки за время dt . По формуле (2.11.1)

Є 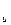= 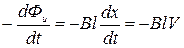. ( 2.11.2 )

Знак минус в формуле показывает, что, возникшая в контуре э.д.с., создает ток, направление которого с выбранным направлением нормали связано правилом левого винта.

Если замкнутый контур, в котором индуцируется э.д.с., состоит не из одного витка, а из N витков, то результирующая э.д.с. будет равна сумме э.д.с., индуцируемых в каждом из витков. И если магнитный поток через каждый виток одинаков и равен 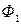, суммарный поток сквозь поверхность, натянутую на такой сложный контур 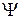можно представить

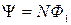( 2.11.3 )

и э.д.с. индукции будет равна

Є 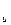= 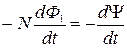. (2.11.4 )

Максвелловская трактовка явления электромагнитной индукции.

Возникновение индукционного тока, очевидно, связано с некой силой, которая заставляет направлено двигаться заряды проводника. Когда проводник движется в постоянном магнитном поле, - это магнитная составляющая силы Лоренца (2.8.1), которая действует только на движущиеся заряды. Какая же сила порождает электрический ток в неподвижном проводнике? Ответ был дан английским физиком Дж.Максвеллом. Он предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле. Причем, поскольку, как будет показано далее, циркуляция вектора напряженности такого поля отлична от нуля, это поле является не потенциальным, а вихревым. Таким образом, возникает электрическая составляющая обобщенной силы Лоренца, которая и вызывает направленное движение зарядов.

С учетом определения э.д.с. (2.6.17) и формулы (2.11.1) запишем

Є 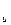= 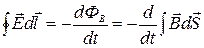. (2.11.5 )

В правой части этого соотношения время и координаты – независимые переменные. Поэтому производную по времени и интеграл можно поменять местами, что приведет к уравнению

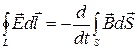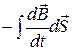= . (2.11.6 )

Самоиндукция. Взаимная индукция.

Частным случаем электромагнитной индукции является самоиндукция. Рассмотрим тонкий замкнутый провод, по которому течет ток. Этот ток создает магнитное поле во всем пространстве и, в частности, в области окруженной проводником. Если будет изменяться сила тока или конфигурация провода, то будет меняться магнитный поток (собственный магнитный поток), что приведет к появлению в проводе индукционного тока, который, в свою очередь, изменит ток, текущий по проводнику. Это явление называется самоиндукцией. По определению магнитный поток пропорционален вектору , а он пропорционален силе тока, кторый создает магнитное поле. Поэтому магнитный поток пропорционален силе тока, текущего по проводнику. Можно ввести коэффициент пропорциональности, называемый коэффициентом самоиндукции или индуктивностью. Эту величину обычно обозначают L . Тогда запишем

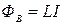, ( 2.11.7 )

и э.д.с. самоиндукции Є = 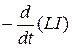. ( 2.11.8 )

Индуктивность зависит от формы и размеров проводящего контура и от магнитной проницаемости среды. Единицей индуктивности в системе СИ является генри (Гн). Если индуктивность не меняется с течением времени, то

Є = 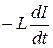. ( 2.11.9 )

Рассчитаем индуктивность бесконечного соленоида, у которого на единицу длины приходится n витков. Длина соленоида l , площадь его поперечного сечения S. Полное число витков N. (Соленоид полагаем бесконечным, если его длина много больше диаметра). Если магнитная проницаемость сердечника соленоида 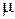, то согласно (2.9.4) модуль В равен 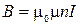и потокосцепление 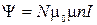S. Отсюда получим

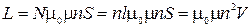, ( 2.11.10 )

где V - объем соленоида.

По правилу Ленца дополнительный ток, возникающий вследствие самоиндукции, всегда направлен так, чтобы противодействовать изменению тока в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании происходит не мгновенно, а постепенно. Как показывают расчеты, и нарастание и убывание тока происходят по экспоненциальному закону, а скорость изменения силы тока определяется имеющей размерность времени величиной 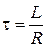- временем, в течение которого сила тока изменяется в е раз. Что касается размыкания тока, то приведенный результат справедлив, если в момент отключения источника цепь замыкается накоротко. Если просто разорвать цепь с большой индуктивностью, возникающее высокое индуцированное напряжение создает искру или дугу в месте разрыва. Этот эффект всегда учитывается в электротехнике.

Другим частным случаем электромагнитной индукции является взаимная индукция. Рассмотрим два неподвижных контура 1 и 2, расположенных достаточно близко друг к другу. Если в контуре 1 течет ток 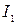, он создает в пространстве, ограниченном контуром 2, магнитное поле, а следовательно, через поверхность, ограниченную вторым контуром существует магнитный поток 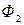, пропорциональный току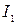

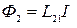. ( 2.11.11 )

При изменении тока в первом контуре - во втором индуцируется э.д.с.

Є 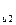= 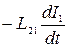. ( 2.11 12 )

Это явление называется взаимной индукцией, а коэффициент пропорциональности 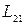- коэффициентом взаимоиндукции или взаимной индуктивностью.

Очевидно, что контуры можно переобозначить, и тогда в контуре 1 возникнет э.д.с. индукции при изменении тока в контуре 2

Є 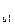= 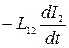. ( 2.11.13 )

Соответствующий расчет дает (и опыт его подтверждает), что в отсутствие ферромагнетиков коэффициенты пропорциональности в (2.11.12) и (2.11.13) равны 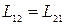. ( 2.11.14 )

Их величина зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости окружающей среды. Поэтому можно не делать различия между 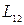и 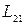, а просто говорить о взаимной индуктивности контуров.

В заключение отметим, что на явлении электромагнитной индукции основано большое число технических устройств: генераторы электрического тока, электромоторы индукционного действия, трансформаторы и т.д.

Энергия проводника с током. Энергия магнитного поля.

Рассмотрим проводник, имеющий индуктивность L и сопротивление R , который с помощью ключа можно подключить к источнику с э.д.с. Є и нулевым внутренним сопротивлением. В момент замыкания ключа по цепи потечет ток I . Для этого контура можно написать закон Ома

IR=Є+Є =Є .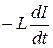

Отсюда можно выразить э.д.с. источника и рассчитать его работу за все время установления тока в цепи

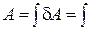Є 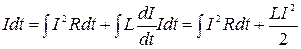. ( 2.11.15 )

Первое слагаемое в полученном выражении определяет количество тепла, выделившееся при протекании тока по проводнику. Но ток в проводнике создает в окружающем пространстве магнитное поле и , по-видимому, второе слагаемое в (2.11.15) определяет ту часть работы источника, которая перешла в энергию магнитного поля. Таким образом, энергия проводника с током (или энергия индуктивности) будет находиться

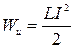. ( 2.11.16 )

Фактически это – энергия магнитного поля, созданного проводником с током. Выразим эту энергию через величины, характеризующие поле. Для этого рассмотрим простейший случай бесконечно длинного соленоида. Используя формулы (2.10.8) и (2.9.4), получим, что напряженность поля внутри такого соленоида 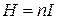. Выражая отсюда силу тока и зная, что индуктивность соленоида определяется (2.11.10), получим

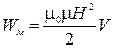. ( 2.11.17 )

Здесь V - объем пространства внутри соленоида, т.е. пространства, занятого магнитным полем. Тогда, разделив энергию на объем, получим выражение для объемной плотности энергии магнитного поля (энергии в единице объема) 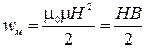. ( 2.11.18 )

В общем же случае для любого магнетика объемная плотность энергии магнитного поля рассчитывается

. ( 2.11.19 )