Колебательный контур.

Колебательный контур. Собственные колебания в контуре.

В цепи, содержащей катушку индуктивности L и конденсатор емкости C, могут возникнуть электрические колебания. Поэтому такую цепь называют колебательным контуром. Выясним, каким образом в колебательном контуре возникают и поддерживаются электрические колебания.

Пусть вначале верхняя обкладка конденсатора заряжена положительно, а нижняя отрицательно (рис.а). При этом вся энергия колебательного контура сосредоточена в конденсаторе. Замкнем ключ K. Конденсатор начнет разряжаться, и через катушку L потечет ток, который будет постепенно нарастать Рис.2.15.1.

за счет явления самоиндукции в катушке. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума (рис. б). С этого момента ток, не меняя направления, начнет убывать (опять за счет самоиндукции) Однако он прекратится не сразу — его будет поддерживать э.д.с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на конденсаторе достигнет максимума, но теперь верхняя обкладка будет заряжена отрицательно, а нижняя – положительно. С этого момента конденсатор начнет разряжаться опять, ток потечет в обратном направлении и т. д. — процесс будет повторяться.

В контуре при отсутствии сопротивления проводников будут совершаться строго периодические незатухающие колебания. В ходе процесса периодически изменяются заряд на обкладках конденсатора, напряжение на нем и ток через катушку. Колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей.

Уравнение, описывающее такие колебания, получим, если приравняем разность потенциалов на конденсаторе и катушке

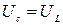
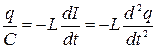
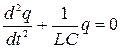. ( 2.15.1 )

Сравнивая это уравнение с (2.13.8), получаем, что циклическая частота собственных незатухающих колебаний в колебательном контуре

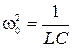. ( 2.15.2 )

Если же сопротивление проводников в колебательном контуре R ≠ 0, то помимо описанного процесса будет происходить преобразование электромагнитной энергии в джоулево тепло. Потеря энергии приведет к затуханию колебаний в контуре. Сопротивление проводников цепи R принято называть активным сопротивлением.

Вынужденные колебания в колебательном контуре.

Как мы знаем, для получения незатухающих колебаний в реальной системе необходимо воздействие некоторой вынуждающей силы. Роль такой силы в колебательном контуре играет включение в него источника переменного напряжения, меняющегося по гармоническому закону. Э.д.с. этого источника Є.

Найдем уравнение колебаний в контуре, содержащем последовательно соединенные конденсатор C, катушку индуктивности L, активное сопротивление R и внешнюю переменную э.д.с. (см. рисунок).

Прежде всего, выберем положительное направление обхода контура, например по часовой стрелке. Обозначим через q заряд той обкладки конденсатора, направление от которой к другой Рис.2.15.2.

обкладке совпадает с выбранным положительным направлением обхода контура. Тогда ток в контуре определяется как

I=dq/dt. (2.15.3 )

Следовательно, если I > 0, то и dq > 0, и наоборот (знак I совпадает со знаком dq).

Согласно закону Ома для участка цепи 1RL2

RI=φ₁ – φ₂ + Є + Є, ( 2.15.4 )

где Є — э.д.с. самоиндукции. В нашем случае

Є = - L dI/dt, φ₁ – φ₂ = q/C

(знак q должен совпадать со знаком разности φ₁ – φ₂, ибо C > 0). Поэтому уравнение (2.15.4) можно переписать в виде

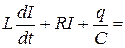Є, ( 2.15.5 )

или с учетом (2.15.3) как

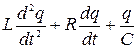=Є ( 2.15.6 )

Это линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами. Найдя с помощью этого уравнения q(t ), мы можем легко вычислить напряжение на конденсаторе как U_C = φ₂ – φ₁ = q/С и силу тока I — по формуле (2.15.3).

Уравнению колебательного контура можно придать иной вид:

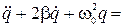Є/L, ( 2.15.7 )

где 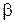- коэффициент затухания

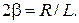( 2.15.8 )

Если э.д.с. источника Є=Є 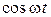, то (2.15.7 ) перепишется

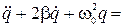(Є /L) 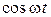. ( 2.15.9 )

Решение этого уравнения по аналогии с (2.13.19) запишется

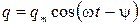( 2.15.10 )

где q_m — амплитуда заряда на конденсаторе; ψ — разность фаз между колебаниями заряда и внешней э.д.с. Эти величины определяются только свойствами самого контура и вынуждающей э.д.с В соответствии с (2.13.20) и (2.13.21) и введя обозначение 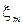=Є /L, можно записать

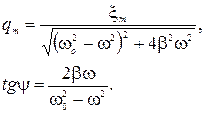( 2.15.11 )

Продифференцировав (2.15.10)) по t, найдем

.

Для дальнейшего удобнее записать это выражение так:

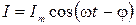( 2.15.12 )

где I_m — амплитуда тока, φ — сдвиг по фазе между током и внешней э. д. с.

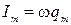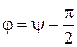; . ( 2.15.13 )

С учетом (2.15.11) 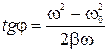. ( 2.15.14 )