Переменный ток.

Ток и напряжение в цепи переменного тока.

Установившиеся вынужденные электрические колебания можно рассматривать как протекание в цепи, обладающей емкостью, индуктивностью и активным сопротивлением R, переменного тока. Под действием внешнего напряжения (оно играет роль внешней э.д.с. )

. ( 2.16.1 )

Cила тока в такой цепи определяется формулой (2.15.12), где с учетом выражений (2.15.13), (2.15.11), (2.15.8) и (2.15.2) амплитуда силы тока

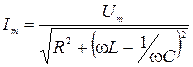, ( 2.16.2 )

А разность фаз между колебаниями тока и внешнего напряжения

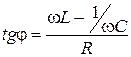. ( 2.16.3 )

Запишем напряжения на отдельных участках цепи: на резисторе - 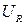, конденсаторе - 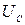и катушке индуктивности -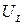

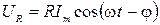, ( 2.16.4 )

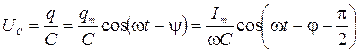, ( 2.16.5 )

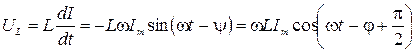. ( 2.16.6 )

Векторная диаграмма.

Из последних трех формул видно, что колебания напряжения на резисторе U_R совпадают по фазе с колебаниями тока I, на конденсаторе 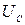отстают по фазе от I на π/2, анна индуктивности U_L опережают I на π/2. Все это можно наглядно представить с помощью векторной диаграммы. Возьмем в качестве прямой, от которой отсчитывается начальная фаза, ось токов. Амплитуды напряжений

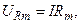
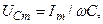
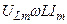
изображаются векторами, представленными на рис.2.16.1, Рис.2.16.1.

а их векторная сумма – результирующее, т.е. внешнее, напряжение.

Из прямоугольного треугольника этой диаграммы легко получить выражения для амплитуды тока (2.16.2) и разности фаз между током и напряжением источника (2.16.3).

Заметим, что полученная нами векторная диаграмма оказывается весьма полезной при решении многих конкретных вопросов. Она позволяет наглядно, легко и быстро анализировать различные ситуации.

Импеданс. Активное и реактивное сопротивление.

Полученное выражение для амплитуды силы тока I_m(ω) можно формально толковать как закон Ома для амплитудных значений тока и напряжения. Стоящую в знаменателе этого выражения величину, имеющую размерность сопротивления, обозначают буквой Z и называют полным сопротивлением или импедансом:

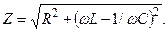(2.16.7 )

Видно, что при 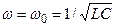это сопротивление минимально и равно активному сопротивлению R. Величину, стоящую в круглых скобках формулы (2.16.7), обозначают Х и называют реактивным сопротивлением:

( 2.16.8 )

При этом величину ωL называют индуктивным сопротивлением, а величину 1/ωC — емкостным сопротивлением. Их обозначают соответственно Х_L и Х_C. Итак,

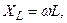
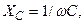X=X_L-X_C, 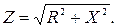( 2.16.9 )

Необходимо отметить, что полученное выражение для импеданса справедливо лишь для последовательного соединения элементов цепи. Для других видов соединения импеданс рассчитывается по другим формулам.

Реактивное сопротивление измеряют в тех же единицах, что и активное, однако, между ними существует принципиальное различие. Оно заключается в том, что только активное сопротивление определяет необратимые процессы в цепи, такие, например, как преобразование электромагнитной энергии в джоулеву теплоту.

Заметим, что индуктивное сопротивление растет с увеличением частоты ω, а емкостное — уменьшается. Когда говорят, что в цепи отсутствует емкость, то это надо понимать в смысле отсутствия емкостного сопротивления, которое равно 1/ωC и, следовательно, обращается в нуль, если C → ∞ (при замене конденсатора закороченным участком).

Как видно из выражения (2.16.2), амплитуда силы тока имеет максимальное значение при ωL-1/ωC = 0. Следовательно, резонансная частота для Рис.2.16.2.

силы тока совпадает с собственной частотой контура:

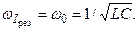( 2.16.10 )

Максимум при резонансе оказывается тем выше и острее, чем меньше коэффициент затухания β = R/2L (рис.2.16.2).

Явление резонанса в нашем случае — это возбуждение сильных колебаний при частоте внешней э.д.с. или напряжения, равной или близкой к собственной частоте колебательного контура. Резонанс используют для выделения из сложного напряжения нужной составляющей. На этом основана вся техника радиоприема. Для того чтобы радиоприемник принимал интересующую нас радиостанцию, его необходимо настроить, т. е. изменением C и L колебательного контура добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией.

С явлением резонанса связана и опасность: внешняя э.д.с. или напряжение могут быть малы, однако при этом напряжения на отдельных элементах контура (на емкости или индуктивности) могут достигать опасного для жизни значения. Об этом необходимо всегда помнить!