Лекция 8 Переменный ток.
§8 - 1Получение переменного тока.
Переменнвм током называется ток, направление которого периодичемки изменяется с течением времени. Основным устройством, которое используется для получения перемен-
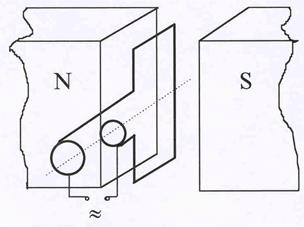 Рис.28. Схема устройства электро-
генератора.
Рис.28. Схема устройства электро-
генератора.
| ного тока, служит электрогенератор. Его дей-ствие основано на явлении электромагнитной индукции. Схема, поясняющая принцип ус-тройства электрогенератора, изображена на рис.28. Прямоугольная рамка помещается в зазор между полюсами магнита N и S так, что она может вращаться вокруг оси, проходящей через ее середину.Т.к. величины вектора маг-нитной индуцкии и площади рамки остаются постоянными, величина ЭДС электромагнит-
ной индукции (см. прошлую лекцию) определяется выражением
E = - 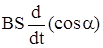 , ,
|
где a - угол между направлением магнитного поля В и нормалью к площади рамки S. На-правление тока в рамке в выбранный момент времени определяется по правилу правой руки. Нетрудно видеть, что направление токов в верхнем и нижнем проводниках противо-положны друг другу. Концы рамки подключаются к кольцам, которые, в свою очередь, с помощью скользящих контактов подсоединены к выходным клеммам генератора. В мощных генераторах рамка содержит несколько десятков или сотен витков, токи в ней достигают значительной величины, поэтому сама рамка делается неподвижной, чтобы избе-жать трущихся контактов, а магнитная система вращается вокруг рамки. Частота вращения является госудаоственным стандартом: в США это 60Гц , в Росси –50 Гц.
§ 8 –2 Квазистационарные токи.
Квазистационарным называется переменный ток, для которого в любой омент времени оказывается справедливым закон Ома, сформулированный ранее для постоянного тока. Это означает, что в неразветвленных цепях сила тока, проходящего через любой элемент цепи, в данный момент времени одинакова для всех элементов. Неквазистационарными токи становятся тогда, когда частота колебаний достигает очень больших значений – таких, что соответствующая им длина волны l = сТ, где с –скорость света, а Т –период колебаний, становится сравнимой с геометрическими размерами цепи. Например, для промышленного тока 50 Гц эта длина волны равна 6000 км.
В прошлом семестре было показано, что на длине волны амплитуды колебаний в разных точках пространства различны, изменяясь от максимума до нуля и нооборот через каждые l/4. Поэтому мгновеннве значения ока будут одинаковы тогда, когда l>> l , где l – длина цепи.
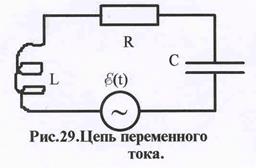
| § 8 –3 Закон Ома для переменного тока. Рассмотрим цепь, состоящую из омического соп-ротивления, катушки индуктивности и конденса-тора. Пусть все они соеденены друг с другом пос-ледовательно и подключены к источнику перемен-ного тока с ЭДС E (см. рис. 29). Формально эта цепь разомкнута, и ее концами являются обкладки конденсатора, поэтому длч нее можно написать закон Ома для участка цепи, содержащей ЭДС, по- |
лагая, что условие квазистационарности выполнено. Тогда
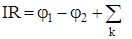 Ek , ( ХХ)
Ek , ( ХХ)
где 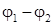 = UC - напряжение на конденсаторе, а суммарная ЭДС складывается из ЭДС источника тока и ЭДС самоиндукции EL :
= UC - напряжение на конденсаторе, а суммарная ЭДС складывается из ЭДС источника тока и ЭДС самоиндукции EL :
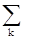 Ek = EL + E (t), EL = -
Ek = EL + E (t), EL = - 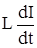 .
.
Обычно величину 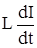 называют падением напряжения на индуктивности и обозна-чают UL , т.е. UL=
называют падением напряжения на индуктивности и обозна-чают UL , т.е. UL= 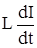 , произведение IR =UR –падением напряжения на сопротивлении. С учетом этого уравнение (ХХ) можно преобразовать:
, произведение IR =UR –падением напряжения на сопротивлении. С учетом этого уравнение (ХХ) можно преобразовать:
UR + UL + UC = E (t). (ХХХ)
Вспоминая, что 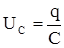 и заменяя величины UC и UL , получим
и заменяя величины UC и UL , получим
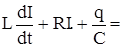 E (t). (¨¨¨)
E (t). (¨¨¨)
Предположим, что ток в нашей цепи изменяется по синусоидальному закону: I = I0 sinwt.
Тогда UR = I0R sinwt , UL = wLI0 coswt = wLI0 sin(wt -p/2),
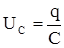 =
= 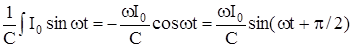 .
.
Эти соотношения должны быть спаведливыми в любой момент времени, поэтому они спра-ведливы и для амплитудных значений, т.е.
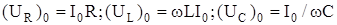 .
.
Трактуя эти равенства как закон Ома для участка цепи, можно заметить, что величины ZL =wL и ZC = 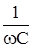 аналогичны по своему значению сопротивлению R. Используя такую
аналогичны по своему значению сопротивлению R. Используя такую
интерпретацию, можно видеть, что уравнение (¨¨¨) приобретает тригонометрический смысл: напряжения на емкости и индуктивности оказываются сдвинутыми по фазе на ±p/2 относительно напряжения на сопротивлении R. Здесь удобнее использовать векторное представление колебаний, которое рассматривалось в прошлом семестре. Любое гармо-ническое колебание y(t) = Asin( wt + j) можно представить в векторном виде: длина вектора определяется амплитудой колебаний А, начальная фаза определяет угол отклонения вектора от горизональной оси, а w - частоту, с которой вектор вращается вокруг начала координат. В этом представлении напряжение на сопротивлении R изображается в виде горизонтально-
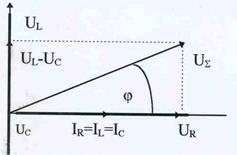 Рис.30. Векторная диаграмма
для последовательной цепи.
Рис.30. Векторная диаграмма
для последовательной цепи.
| го вектора (см. рис.30), а напряжения на емкости и индуктивности оказываются повернутыми относи-тельно него в разные стороны на 900 . В последова-тельной цепи действующее в ней общее напряжение складывается из падения напряжений на всех участ-ках. Поэтому оно может быть найдено как геомет-рическая сумма падения напряжений на индуктив-ности, емкости и сопротивления. Тогда согласно тео-реме Пифагора можно записать, что
 , ,
|
или, выражая UR , UL и UC через произведения тока на соответствующие сопротивления,
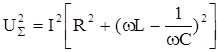 .
.
Извлекая квадратный корень из обеих частей последнего равенства, получим:
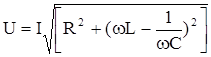 . (·)
. (·)
При выводе этого выражения учтено, что для последовательной цепи IR = IL= IC =I. Полученное выражение по своей структуре аналогично закону Ома для цепи постоянного тока. Поэтому оно называется законом Ома для переменного тока. Важно отметить, что между током и напряжением существует сдвиг фаз, величина которого определяется из рис.30:
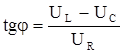 или
или 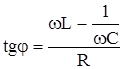 .
.
§ 8 – 4 Мощность переменного тока.
Значение мгновенной мощности W определим по аналогии с законом Джоуля – Ленца для постоянного тока: W =IU = I0U0 sinwt sin(wt +j). Однако, с практической точки зрения более полезно вычислить среднюю мощность за единицу времени. Определим среднее значение за время одного колебания любой переменной величины y(t) как интеграл, средний за период: 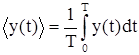 . Тогда
. Тогда 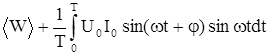 =
=
= 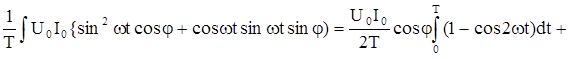
+ 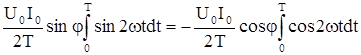 = -
= - 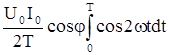 +
+
+  .
.
Интегралы в последнем выражении все равны нулю, т.к. среднее значение за период лю-бой периодической величины равно нулю.Поэтому 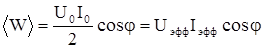 , где Uэфф=
, где Uэфф= 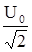 ; Iэфф =
; Iэфф = 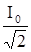 - так называемые эффективные значения напряжения и тока.
- так называемые эффективные значения напряжения и тока.
Формула мощности для переменного тока отличается от аналогичной формулы для постоянного тока лишь коэффициентом cosj , который принято называть коэффициентом мощности. Увеличение этого коэффициента является важной практической задачей. Там, где сдвиг фаз между током и напряжением достигает 900 , средняя мощность оказывается равной нулю.
Лекция 9 Колебательный контур.. §9 –1 Затухающие колебания в колебательном контуре.
Рассмотрим последовательную цепь, содержащую катушку индуктивности L, ем-кость С, сопротивление R и ключ. Предположим, что на емкости в начальный момент вре-мени имеется некоторый заряд . Если цепь замыкается, то в цепи возникает электрический ток. Наличие катушки индуктивности обуславливает возникновение ЭДС самоиндукции, которая своим действием препятствует возрастанию разрядного тока конденсатора. В тот момент, когда напряжение на конденсаторе становится равным нулю, ток через индуктив-ность достигает максимума. В дальнейшем ЭДС самоиндукции стремится поддержать этот ток, что приводит к перезарядке конденсатора до некоторого напряжения обратной поляр-ности. Процесс перезарядки конденсатора повторяется определенное число раз в зави-симости от величины потерь энергии на сопротивлении. Способность контура к переза-рядке характеризуется качеством контура или добротностью. Добротность контура Q опре-деляется отношением энергии, запасенной на конденсаторе или в катушке индуктивности, к величине потерь энергии на сопротивлении за период:
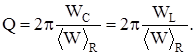
Для количественного описания процессов в последовательном колебательном кон-туре используется уравнение, полученное ранее при рассмотрении переменного тока:
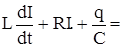 E (t), ( ++)
E (t), ( ++)
с той разницей, что в нашем случае внешняя ЭДС отсутствует так, что уравнение прини-мает вид:
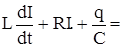 0.
0.
Введем обозначения : 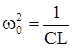 ; b =
; b = 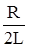 и учтем, что по опеределению I=
и учтем, что по опеределению I= 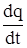 .Тогда наше уравнение принимает вид, знакомый по курсу прошлого семестра:
.Тогда наше уравнение принимает вид, знакомый по курсу прошлого семестра:
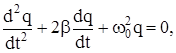
где в качестве переменной выступает заряд q. Решением этого дифференциального урав-нения служит функция q(t) = q0 e -bt cos(wt + j), где величины q0 и j определяются началь-ными условиями  , а w2 =
, а w2 = 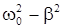
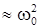 с учетом того, что в большинстве случаев b<<w0 . Очевидно, что при b = 0 колебания в контуре становятся незатухающими, и частота этих колебаний равна
с учетом того, что в большинстве случаев b<<w0 . Очевидно, что при b = 0 колебания в контуре становятся незатухающими, и частота этих колебаний равна 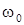 . Добротность контура Q может быть выражена через его пара-метры. Энергия, запасенная в индуктивности, равна L
. Добротность контура Q может быть выражена через его пара-метры. Энергия, запасенная в индуктивности, равна L 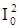 /2., а мощность, выделяемая на сопротив-лении, -
/2., а мощность, выделяемая на сопротив-лении, - 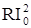 /2. За период Т =
/2. За период Т = 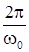 на сопротивлении выделится энергия R
на сопротивлении выделится энергия R 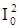 T/2 = p
T/2 = p 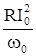 . Поэтому Q = 2p
. Поэтому Q = 2p 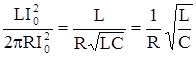 .
.
Как видно из полусенного выражения, величина добротности определяется лишь парамет-рами контура L,C и R.
§9 –2 Вынужденные колебания в контуре. Резонанс.
Включим в цепь рассматриваемого контура внешнюю переменную ЭДС E = E0 sin(wt+j).
Повторяя процедуру прошлого семестра, найдем графическое решение уравнения (++). Бу-дем искать решение уравнения
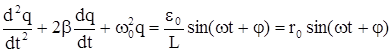
в виде q(t) = q0sin wt. Тогда
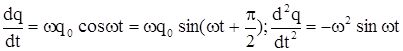 .
.
Подставляя эти величины в исходное уравнение, имеем:
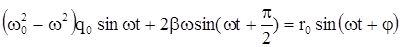 .
.
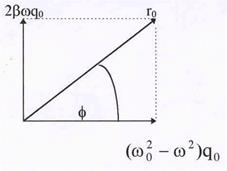 Рис.31.Графическое решение
дифференциального уравнения.
Рис.31.Графическое решение
дифференциального уравнения.
| Обращаясь к векторному представлению колебаний, нетрудно заметить, что вектор r0 , стоящий в правой части уравнения является суммой двух других векто-ров, представляющих колебания в левой части. Из рис.31 по теореме Пифагора
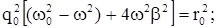 откуда
откуда
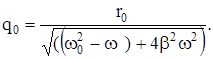 (Р) (Р)
|
Из полученного выражения видно, что амплитуда заряда на конденсатора изменяется в зависимости от частоты внешней ЭДС, достигая максимума, когда подкоренное выражение минимально. Это достигается тогда, когда 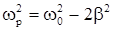 ; если b<<w0 , то wР » w0
; если b<<w0 , то wР » w0
называется резонансной частотой. В момент резонанса q0 =  , и напря-жение на конденсаторе
, и напря-жение на конденсаторе
 (*)
(*)
в Q раз больше,чем напряжение внешней ЭДС. Графическая зависимость напряжения на
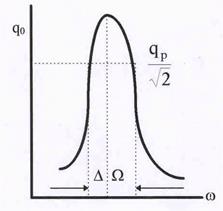 Рис.32. Резонансная кривая.
Рис.32. Резонансная кривая.
| конденсаторе UC от частоты представлена на рис.32. Важной технической характеристикой контура является полоса пропускания, которая определяется как область частот DW,где энергия, запасаемая в контуре на частоте w, отличается от энергии на частоте w0 в наименьшее целое число раз (в два). Обычно DW 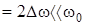 .На границах области .На границах области 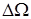 w =w0 ± w =w0 ± 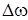 ..При этих условиях ..При этих условиях
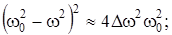
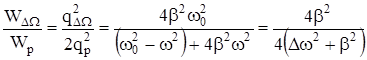 . .
|
Из этого соотношения следует, что Dw =b. Тогда напряжение на емкости можно записать так:
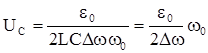 .
.
Сравнивая это выражение с формулой (*), можно заметить, что Q = 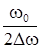 . Последняя фор-мула имеет важный практический смысл. Она позволяет расчитать добротность из экспери-ментально полученной резонанмной кривой. Для этого достаточно провести горизонталь-ную прямую на уровне
. Последняя фор-мула имеет важный практический смысл. Она позволяет расчитать добротность из экспери-ментально полученной резонанмной кривой. Для этого достаточно провести горизонталь-ную прямую на уровне 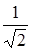 qрез до пересечения с резонансной кривой и спроектировать точки пересечения на ось частот. Этот интервал и определит полосу пропускания.
qрез до пересечения с резонансной кривой и спроектировать точки пересечения на ось частот. Этот интервал и определит полосу пропускания.
Колебательные контура широко применяются в телевизорах, радиоприемниках, передатчиках, в раздичных радиоустройствах избирательного действия и т.п. Мы же рас-смотрим более подробно одно из атмосферных явлений, которое можно представить как разряд конденсатора в колебательном контуре. Это явление – гроза, точнее возникновение молнии.
§9 –3 Простешая теория грозы.
Дождь, как известно, обусловлен тем, что вертикальные потоки нагретого влажного воздуха переносят влагу в верхние слои атмосферы, где водяные пары конденсируются в мельчайшие капельки. Током воздуха капельки увлекаются вверх, постепенно увеличиваясь в своих размерах. Объем (вес) капельки растет пропорционально кубу ее радиуса, тогда как подъемная сила воздушного потока пропорциональна всего лишь квадрату радиуса капли. Поэтому наступает момент, когда капля перестает подниматься и начинает падать. При па-дении капли образуют целый поток, который выталкивает перед собой холодный воздух из верхних слоев атмосферы. Когда капли достигают поверхности Земли, образуется дождь. Началу дождя предшествует холодный вихрь. Возникновение же грозы зависит от того, переносят капли электрический заряд или не переносят. Описание механизма переноса заряда предложено американским ученым Вильямсом. Согласно его гипотезе все опре-деляется структурой грозового облака. Полеты самолетов внутрь таких облаков показали,
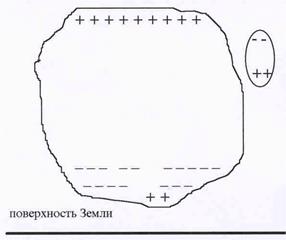 Рис.33. Структура грозового облака.
Рис.33. Структура грозового облака.
| что разные части облака несут разный заряд (см. рис.33). Нижний слой тучи, как правило, несет отрицательный заряд, однако в середине слоя существует область положительного заря-да. Эта область – своебразное сердце грозы. Существующее вокруг ее электрическое поле ионизирует окружающий воздух, постоянно порождая положительные и отрицательные за-ряды.Дождевые капли, двигаясь к Земле, поля-ризуются. Земля несет отрицательный заряд, поэтому на нижней части капли возникает по-ложительный заряд. Увеличенное изображение капли приведено в правой части рисунка. При движении капли вниз – ее нижняя часть поло-жительна, - и она притягивает отрицательные |
ионы, тогда как положительные ионы отталкиваются. Верхняя же часть капли оказывает на ионы меньшее влияние.В результате капли притягивают отрицательные тоны и при-обретают отрицательный заряд. Положительный же заряд переносится в верхнюю часть ту-чи и постепенно переходит в ионосферу. Накопление заряда в различных частях грозового облака приводит к появлению огромной разности потенциалов, достигающей 100 млн Вольт. Эта разность потенциалов может образовываться как между различными облаками, так и между облаком и земной поверхностью. Рассмотрим второй случай. По мере накоп-ления заряда в нижней части облака вблизи его нижней кромки образуется электрическое поле, которое ионизирует воздух. Поле различно в разных точках, поэтому и степень поляризации будет различной. Там, где воздух ионизируется полностью, образуется новое состояние вещества – плазма. Плазма начинает светиться и для уменьшения потерь энергии на излучение стремится образовать шарообразную форму. Внешне это выглядит так: из тучи внезапно вываливается небольшой светящийся комок, получивший название белого лидера, и устремляется к Земле. Скорость его движения достигает 50 000 км/сек. Но лидер двигается с остановками, во время которых может произойти его деление. Движение лидера подготавливает канал для основного разряда. Если лидер делится, то возможно ветвление разряда. Когда до Земли остается около 100 метров, с земной поверхности навстречу лидеру поднимается заряд, стремящийся двигаться вдоль острых высоких предметов. При смы-кании лидера с этим зарядом образуется канал, по которому отрицательный заряд попадает на Землю. Образуется гигантская искра, но длительность этого искрового разряда мала. Через доли секунды из тучи выходит новый комок – так называемый темный лидер. Он с большой скоростью и без остановки устремляется к Земле по подготовленному каналу. Вслед за ним идет основной разряд. Искра возникает снова. Темный лидер может образовываться несколько раз, вызывая несколько ударов молнии ( рекорд – 42 раза).
Каждый удар молнии переносит до 40 Кулонов, но отрицательный заряд не удержи-вается на Земле. Между земной поверхностью и ионосферой существует разность потен-циалов около 400 киловольт, поэтому в атмосфере постоянно идет ток, направленный вверх. Его плотность мала – несколько микроампер на кв. метр ( 1 мкА = 10 –6 А), но общее значение тока достигает 1800 Ампер. Мощность, развиваемая в такой цепи, превышает 700 Мегаватт. Грозы лишь компенсируют утечку заряда. Ежесекундно на Земле происходит около 300 гроз. Средний разрядный ток в них также равен 1800 Ампер, обеспечивая неизменность заряда Земли.
§ 9 –4 Теория Максвелла.
Рассмотрим проводящий виток, помещенный в изменяющееся магнитное поле. По за-
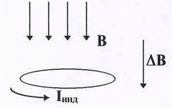 Рис.34. Направление
индукционного тока.
Рис.34. Направление
индукционного тока.
| кону Фарадея в витке возникает ЭДС индукции. Направление индукционного тока таково, что он своим действием препятст-вует изменению магнитного поля. Если внешнее магнитное поле возрастает, его изменение DВ направлено по полю (см. рис.34), и напрвление индукционного тока должно быть таким, чтобы маг-нитный момент витка Iинд S был нап равлен против поля В. Как уже указывалось (§6-4) величина ЭДС индукции определяется выражением |
E = - 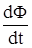 ; Ф =
; Ф = 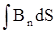 .
.
Если виток не изменяет своей формы, то знак производной можно внести под знак инте-грала. Тогда получим:
E = - 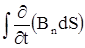 ,
,
где наклонные 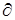 означают частную производную (предполагается, что значения В могут зависить от времени и координат).
означают частную производную (предполагается, что значения В могут зависить от времени и координат).
Согласно своему определению ЭДС характеризует работу, совершаемую стороннми силами по всему замкнутому контуру (витку), т.е. E = 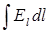 , где Е представляет собой напряженность сторонних сил, создающих индукционный ток. Виток замкнут и однороден, поэтому силовые линии электрического поля тоже должны быть замкнутыми, т.е. индуци-рованное в проводнике электрическое поле является вихревым. Максвелл предположил, что наличие проводника не является обязательным: силовые линии электрического поля останутся замкнутыми и в свободном пространстве. На основании этого он сделал вывод, что всякое изменяющееся во времени магнитное поле порждает вокруг себя вихревое электрическое поле. Это положение называют первой гипотезой Максвелла, Закон Фара-дея теперь записывается так:
, где Е представляет собой напряженность сторонних сил, создающих индукционный ток. Виток замкнут и однороден, поэтому силовые линии электрического поля тоже должны быть замкнутыми, т.е. индуци-рованное в проводнике электрическое поле является вихревым. Максвелл предположил, что наличие проводника не является обязательным: силовые линии электрического поля останутся замкнутыми и в свободном пространстве. На основании этого он сделал вывод, что всякое изменяющееся во времени магнитное поле порждает вокруг себя вихревое электрическое поле. Это положение называют первой гипотезой Максвелла, Закон Фара-дея теперь записывается так:
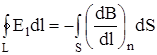 . ( I )
. ( I )
Кроме этого существует второе положеие теории Максвелла, которое вытекает из рассмотрения теоремы о циркуляции магнитного поля. Как было показано, циркуляция магнитного поля имеет следующий вид:
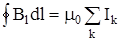 .
.
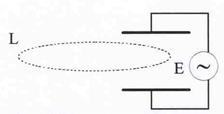 Рис.35. К выводу теоремы о
полном токе.
Рис.35. К выводу теоремы о
полном токе.
| Это значит, что любое магнитное поле порождается то-ками. При рассмотрении переменного тока в цепи, содер-жащей конденсатор, можно было заметить, что линии тока прерываются на его пластинах - в пространстве между пластинами ток отсутствует (см. рис.35). Тогда оказывается, что выбирая контур интегрирования L внут-ри этой области, можно нарушить теорему о циркуляции. Максвелл предоложил, что теорема о циркуляции векто- |
ра магнитной индукции остается справедливой и для контура L за счет того, что в простран-стве между пластинами также имеется некий «волшебный» ток Iволш , причем полный ток в цепи складывается из тока проводимости I пров и этого «волшебного» тока,т.е.
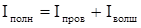 .
.
В проводниках I пров = Iполн , а в пространстве между пластинами Iполн = Iволш . Нетрудно видеть, что при этих условиях теорема о циркуляции справедлива везде.
Обратимся к рассмотрению «волшебного тока» внутри пластин конденсатора. Мы знаем, что ток I пров =dQ/dt. На конденсаторе Q = Ss (s - плотность поверхностных зарядов, а S – площадь пластин конденсатора). Напряженность электрического поля внутри конден-сатора равна E = s/e0 или D0 = s , где D0 = e0 E – вектор электрического смещения. С учетом этого запишем
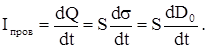
В то же время очевидно, что I пров = Iволш, поэтому последний ток Максвелл назвал током смещения. Теперь теорема о циркуляции принимает новый вид, где под знаком суммы стоит полный ток Iполн:
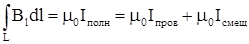 .
.
Для проводников произвольного сечения и для проиэвольной формы пластин конденсатора токи выражаются через соответствующее суммирование плотности токов:
Iпров = 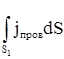 ; I смещ =
; I смещ = 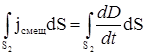 ,
,
так что теорема о полном токе приобретает следующий вид:
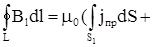
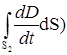 . (II)
. (II)
Если проводники отсутствуют, ток проводимости равен нулю, и уравнение (II) имеет вид:
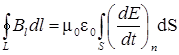 . (III)
. (III)
Таким образом, второе положение теории Максвелла может быть сформулировано так:
Всякое изменяющееся во времени электрическое поле порождает вокруг себя магнитное вихревре поле.
Уравнения (I) и (II) называются уравнениями Максвелла. Вместе с уравнениями
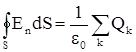 и
и 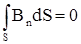 .
.
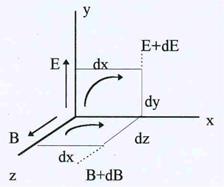 Рис.36. К вычислению цир-
куляций для векторов Е и В. Рис.36. К вычислению цир-
куляций для векторов Е и В.
| они составляют так называемую систему уравнений Мак- свелла, полностью описывающую свойства электрическо- го и магнитного полей. § 9 –5 Электромагнитные волны. Из уравнений Максвелла вытекает вывод о существова-нии электромагнитных волн. Для того, чтобы показать это, рассмотрим уравнения (I) и (III) в применении к кон-кретным полям. Пусть имеется некоторая система коор-динат Х,Y,Z, как показано на рис.36, и в начале координат какими-то внешними причинами созданы электрическое и магнитное поля, характеризующиеся векторами Е иВ соот-ветственно. Направления этих векторов указаны на рис. |
Выберем малые прямоугольники со сторонами dx, dy и dz (см. рис.) Вычислим циркуляции
векторов Е и В по периметру прямоугольников. Для вычисления используем тот же прием, с помощью которого была определена величина вектора магнитной индукции на оси длин-ного соленоида. Направление обхода контуров выберем по часовой стрелке, и учтем, что величины Е и В могут зависеть от х. На расстоянии dx от начала координат они принимают значения Е + dЕ и В + dВ соответственно. При этих условиях
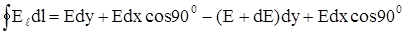 или
или
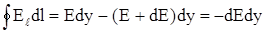 .
.
Аналогично для вектора В
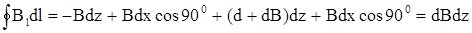 .
.
Значения (E+dE)dy и Bdz взяты со знаком минус потому, что ветора на соответствующих отрезках направлены против выбранного обхода контуров. Подставляя вычисленные значе-ния циркуляции в уравнения (I) и (III), получим:
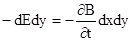 и
и 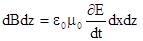 , откуда
, откуда
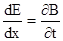 ;
; 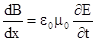 , где производная по х имеет смысл частной произ-
, где производная по х имеет смысл частной произ-
водной, поэтому правильнее заменить знак 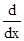 на знак частной производной
на знак частной производной 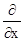 :
:
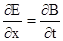 ;
; 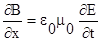 .
.
Диффернецируя первое уравнение по х, а второе – по t, и сравнивая полученные результаты, имеем:

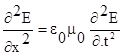 .
.
Из курса механики известно, что это уравнение относится к так называемым волновым уравнениям, решению которых соответствует бегущая волна. Скорость распространения волны определяется коэффициентом, стоящим перед второй производной по времени:
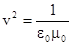 .
.
Аналогичное уравнение может быть получено и для вектора магнитной индукции В.Из ура- внений (I) и (III) следует, что электрический и магнитный вектора связаны между собой, по-
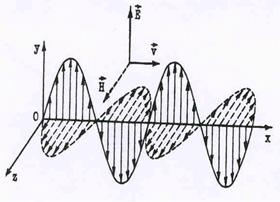 Рис.37. Структура электромагнитной
волны.
Рис.37. Структура электромагнитной
волны.
| этому волны названы электромагнитными. Подставляя численные значения e0 и m0 ,полу-чим,что v = c = 3×108 м/c, т.е. скорость распро-странения электромагнитной волны равна ско-рости света. Если волна распространяется в сре-де, характеризующейся постоянными e и m, то скорость электромагнитной волны
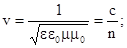 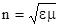 - показатель преломления среды относительно вакуума.
Электромагнитные волны обладают следу-ющими свойствами: - показатель преломления среды относительно вакуума.
Электромагнитные волны обладают следу-ющими свойствами:
|
волны поперечны,т.к. вектора Е иВ направлены по осям Y и Z, тогда как волна распро-страняется вдоль оси Х.
волны поляризованы, т.к. изменяющееся магнитное поле перпендикулярно индуцирован-ному им электрическому.
Это электрическое поле создает переменное магнитное, плоскость колебаний которого сов-падает с плоскостью первичного магнитного поля (см. рис.37) так, что магнитное поле сох-раняет свою ориентацию в пространстве. Если в любой плоскости, перпендикулярной нап-равлению распространения, значения Е и В не зависят от координат, то волна называется плоской, и ее можно записать так:
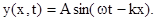
В этом выражении 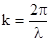 - волновое число, l = сТ, w=2p/T. Формула плоской электромаг-нитной волны будет часто использоваться при рассмотрении оптических явлений. Свето-выми являются волны, длина которых лежит в интервале от 0,4 до 0,7 мкм. Волна, в которой колебания имеют одну частоту, называется монохроматической (одноцветной). Белый свет содержит не менее семи основных цветов. Для упрошения математических выкладок часто ограничиваются рассмотрением монохроматических волн.
- волновое число, l = сТ, w=2p/T. Формула плоской электромаг-нитной волны будет часто использоваться при рассмотрении оптических явлений. Свето-выми являются волны, длина которых лежит в интервале от 0,4 до 0,7 мкм. Волна, в которой колебания имеют одну частоту, называется монохроматической (одноцветной). Белый свет содержит не менее семи основных цветов. Для упрошения математических выкладок часто ограничиваются рассмотрением монохроматических волн.
Дата добавления: 2015-08-08; просмотров: 1583;
