Циркуляция вектора магнитной индукции по закнутому контуру с точностью до пос-тоянного множителя m0 равна алгебраической сумме токов, охватываемых этим контуром.

§ 5 –4 Поле длинного соленоида.

Применим теорему о циркуляции для вычисления поля на оси длинного соленоида. На рис.23 показаны силовые линии магнитного поля для катушки. Мысленно удлиняя ее, можно догадаться, что для достаточно протяженной катушки поле внутри соленоида и снаружи его будет направлено горизонально ( относительно рис.) Выберем контур в виде прямоугольникаАВСD так, чтобы сторона AD лежала на оси соленоида. Тогда циркуляцию

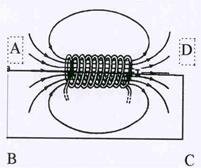Рис.23. Силовые линии магнитного поля соленоида.

вектора магнитной индукции по такому контуру можно представить состоящей из четырех частей: + 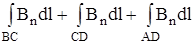. Однако на трех из них значения Вn равны нулю: на отрезках АВ и СD вектор В перпендикулярен этим сторонам, а отре-зок ВС можно удалить в бесконечность, где В = 0. На отрез-ке AD значения В постоянны, и 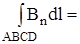ВlC , где l C - дли-на соленоида. Т.к. ток I пересекает контур N раз ( N- число витков) , то Вl C = m0 NI, откуда В =m0 nI, где n =N/ l C .