Лекция 5 Постоянное магнитное поле.

§ 5 –1 Закон Ампера.

Рис.17. Взаимодействие двух элементов тока.

Опыты показывают, что два элемента тока взаимодейству-ют друг с другом. Принятые представления заставляют нас предположить, что это взаимодействие осуществляется посредством поля. Это поле названо магнитным. Изуче-ние свойств этого поля логично бы было проводить по аналогии с электростатическимполем, однако до настоя-щего времени магнитных «зарядов» не обнаружено. При-нято считать, что магнитное поле всегда создается движу-щимися зарядами, т.е. током. Бесконечно малый отрезок проводника, по которому проходит ток, принято называть

элементом тока. Ампером было установлено, что величина сил взаимодействия двух элементов определяется выражением:

, ,

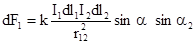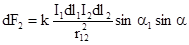где смысл принятых обозначений ясен из рис.17 и 18. Величина k как и прежде введена из соображений размерности. В системе СИ она равна m₀ /4p; значение постоянной m₀ , которую принято называть магнитной постоянной вакуума, записывается так:

m₀ = 4p ´ 10 ^–7 .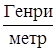

Для определения силы как вектора закон Ампера должен быть изменен так, чтобы справа стояло векторное произведение:

, .

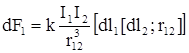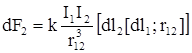По аналогии с электростатическим полем для характеристики магнитного поля можно ввести силовую величину, отнесенную к единичному элементу тока. В теории магнитизма эту величину принято называть магнитной индукцией, точнее вектором магнитной индукции. Тогда закон Ампера для произвольного элемента тока I₂ dl₂ может быть записан как

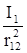dF₂ = I₂ [dl₂ dB], dB = dl₁sina₁ , dB = k 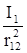[dl₁,r₁₂] .

Это определение как модуля, так и самого вектора dB носит название закона Био-Савара-Лапласа.

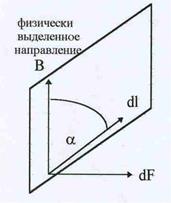Рис.18. Правило право-го винта.

Однако для установления единиц измерения величины макро-скопического вектора B,его удобнее определить несколько иным способом. Пусть исследуемое магнитное поле создается системой проводников, а для измерения силы используется в качестве элемента тока короткий жесткий проводник, соеди-ненный с источником тока гибкими проводами. Сила, действу-ющая на пробный элемент, зависит от его ориентации в прост-ранстве. В каждой точке поля существует физически выделенное направление В, которое замечательно тем, что, во-первых, модуль действующей силы пропорционален синусу угла между этим направлением и направлением элемента тока, и, во-вторых, направление силы связано с направлением элемента тока и физи- чески выделенным направлением В известным правилом право-

го винта:если вращать вектор dl по кратчайшему углу в сторону к физически выделенному направлению, то движение оси винта покажет направление действия силы dF = BIdlsina. В векторной записи

dF = I[dl B].

Сила максимальна, когда dl перпендикулярно направлению В. В этом случае В определя-ется как:

.

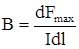Отсюда единица измерения магнитной индукции в системе СИ, называемая тесла, определяется как 1Н/ (1A´1M).

Магнитное поле можно наглядно изобразить с помощью силовых линий, проводя их по тем же правилам, чио и в электростатике, но характер этих линий – другой.

Как уже отмечалось,магнитных зарядов не существует, поэтому свойства силовых линий магнитного поля отличаются от свойств электростатического поля. Из следствия теоремы Гаусса вытекает, что поток вектора Вчерез любую замкнутую поверхность должен равняться нулю, т.е. силовые линии магнитной индукции непрерывны, и

.

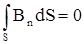Теоретический расчет величины В для конкретной конфигурации проводников произво-дится на основании закона Био-Савара-Лапласа с использованием принципа суперпозиции

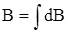, где суммирование произодится по всем проводникам, образующих данную систему.

§ 5 –2 Поле прямого тока и витка с током.

В качестве примеров расчета значений вектора магнитной индукции вычислим поле прямого тока и в центре круглого витка с током.

Поле прямого тока.

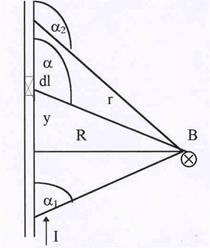Рис.19. Поле прямого тока.

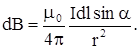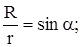Пусть требуется найти поле отбесконечного прямого тока I на расстоянии R от него. Выберем элемент тока dl, как показано на рис.19. Величина модуля вектора определяется выражением Для суммирования свяжем все переменные друг с другом, выбирая в качестве интегрируемой переменной угол a. Из рис.19 видно, что 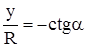; 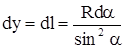. Подставляя эти выражения в формулу для В, после пре-образований получим:

;

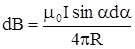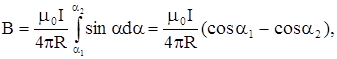
где a₁ и a₂ – углы, соответствующие направлениям на концы проводника. Если проводник

бесконечный, то a₁® 0, а a₂® p, и .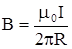

Направление вектора В определяется правилом вычисления векторного произведения: первый сомножитель (dl в нашем случае) вращается в направлении наименьшего угла ко второму сомножителю (r). Направление движения оси правого винта при таком вращении покажет направление их векторного произведения ( на рис.- от нас – значок -Ä). Силовые линии магнитного поля являются концентрическими окружностями, охватывающими про-водник с током. Все они лежат в плоскости, перпендикулярной направлению тока.

Поле витка с током.

Вычислим значение вектора магнитной индукции в центре круглого витка, обтекаемого

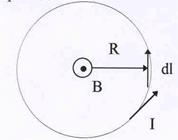Рис.20. Поле в центре витка с током.

током I. Как видно из рис.20, в этом случае элемент тока dl перпендикулярен радиусу R, и суммирование сводится просто к вычислению длины окружности. Поэтому 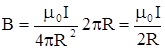. Все элементы тока дают одинаковое направление вектора dB так ,что суммарный вектор В перпендикулярен плоскости чертежа и направлен на нас (значок · ).

§ 5 –3 Теорема о циркуляции магнитного поля.

Пусть имеется тонкий бесконечный провод, по которому проходит ток силой I. Выберем мысленно окружность радиуса R, концентрическую заданному току и лежащую в плоскос-ти, перпендикулярной ему. Рассмотрим сумму произведений проекций вектора магнитной

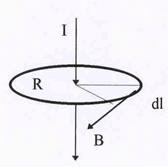Рис.21. Вычисление цир- куляции.

индукции на соответствующий элемент длины окружности ра-диуса R ( рис.21) Bldl. Если суммирование проводится по всей длине окружности, то результат носит название циркуляции, т.е. его можно за-писать так 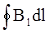.Для выбранного нами контура в виде окруж-ности величина интеграла может быть вычислена непосред-ственно. Во всех точках контура вектора В направлены по касательной к окружности, а значения В постоянны и равны В = 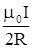, так что его можно вынести за знак интеграла. Тогда

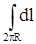= 2pR и циркуляция .

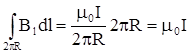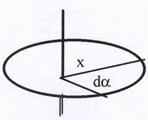Рис.22. К расчету элемента контура.

Если мысленный контур не концентричен току, то результат суммирования не меняется, т.к. для любого элемента контура (см. рис.22) Вl dl = 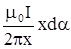и не зависит от расстояния х от тока до элемента контура. Угол da означает малый угол, под которым виден элемент длины контура из точки пересечения его площади током. Очевидно, что полное значение суммирования не изменится и для произвольной формы контура, который удобно в этом случае

представить как ломаную линию, состоящую из элементов окружностей и приращений ра-диуса. Здесь следует помнить, что проекции вектора В на приращения радиуса равны нулю.

Если плоскость, в которой лежит наш мысленный контур, не перпендикулярен на-правлению тока, то контур можно спроектировать на плоскость, нормальную к току, снова результат вычисления циркуляции будет прежний. Если через плоскость нашего контура проходит несколько токов I₁, I₂ и т.д., то поскольку выражение для циркуляции остается справедливым для каждого тока в отдельности, оно останется справедливым и для суммы токов. Итак, в общем можно записать:

.

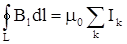Полученное выражение носит название теоремы о циркуляции и является одним из уравнений Максвелла. Суммирование в правой части этого уравнения носит алгебраи-ческий характер: токи могут иметь знак (+) или (-) в зависимости от того, острый или тупой углы образуют они с направлением заданной нормали к площади, охватываемой контуром.

Поля, циркуляция которых отлична от нуля, называются вихревыми.

Словесная формулировка теоремы о циркуляции: