Лекция 13 Законы теплового излучения.
§13 - 1 Закон Кирхгофа.
Обычно тепловым излучением считают электромагнитные волны, длина волны которых лежит в интервале от одного до нескольких десятков микрон (1 мкм = 10 - 6 м). Эти волны, также как и свет, испускаются атомами в виде отдельных цугов, начальная фаза и поляризация которых изменяются хаотически от одного элементарного акта испускания к другому. Поэтому тепловое излучение является некогерентным,и его закономерности ока-зываются справедливыми для всего диапазона электромагнитных волн.
Опыт показывает, что тепловое излучение можно охарактеризовать некоторыми па-раметрами. Известно,например, что интенсивность излучения зависит от температуры. Дру-гим важным свойством излучения является его спектральный состав, т.е распределение ин-тенсивности по различным частотам. Наиболее общей величиной для характеристики теп-лового излучения может служить поток энергии.Количество энергии, приходящееся на еди- ничный интервал частот, которое испускает единица площади (1м2) нагретого тела называетсяизлучателыной способностью:
Е n,Т = d Физл / d n .
Одновременно вводится понятиепоглощательной способности А n,Т , определяемой как отношение поглощенной энергии к падающей,т.е.А n,Т = dФпог / dФпад .Тело, погло-щательная способность которого равна единице.называется абсолютно черным телом.
Между испускательной Е n,Т и поглощательной А n,Т способностями существует
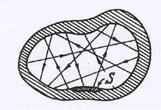 Рис.60.Излучение в зам-
кнутой полости.
Рис.60.Излучение в зам-
кнутой полости.
| определенная взаимосвязь. Для установления этой взаимосвязи рассмотрим некую замкнутую полость, вырезанную внутри изолированного от внешних воздействий тела(см.рис.60). Каждый участок поверхности полости излучает и поглощает лучистую энергию.Согласно законам термодинамики через не-которое время внутри полости наступит равновесие – темпера-тура всех ее частей(и излучения тоже) станет одинаковой. Излучение, находящееся в тепловом равновесии с окружающи- |
ми телами,называетсяравновесным.Опыт показывает, что в природе излучение всегда равновесно, т.е.его интенсивность и спектральный состав в точности соответствует темпе-ратуре излучившего его тела.
Существующий между различными участками поверхности тепловой баланс должен выполняться для всех каналов теплообмена, т.к. в противном случае можно бы было перекрыв любой из них добиться нарушения равновесия,что противоречит законам термо-динамики.В частности.это значит.что равновесие выполняется для каждого частотного интервала. Выделим внутри полости некоторую площадку S, излучательная способность которой равна Еn,Т, а поглощательная - Аn,Т , и пусть на эту площадку падает поток энергии dФпад.B интервале частот от n до n+ dn площадка излучает поток энергии dФизл = Еn,Т Sdn и поглощает dФпог = Аn,ТdФпад.В равновесии dФизл = dФпад. Из этого следует: dФпад = 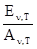 dnS .
dnS .
Заменим теперь площадку S участком поверхности абсолютно черного тела с излучатель-ной способностью en,Т .Равновесие от этого нарушится не должно, и поток падающей энер-гии должен сохранить свое значение: dФпад = en,Т S d n. Сравнивая это выражение с выраже-нием для падающего потока энергии на площадку S, получим:
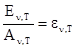
т.е. отношение испускательной и поглощательной способностей остается постоянным для любого тела.. Другими словами, их отношение есть универсальная функция частоты и температуры.Это положение носит названиезакона Кирхгофа.
§ 13 - 2 Вывод выражения для излучательной способности.
Это выражение впервые было получено М.Планком, который, опираясь на известный ему экспериментальный материал, предположил, что энергия световой волны пропорциональна не квадрату ее амплитуды, а частоте n, т.e. Есв = hn , где h - коэффициент пропорциональности, известный теперь как постоянная Планка ( h = 6,62× 10 -34 Дж сек.), причем про-цесс излучения происходит не непрерывно, а отдельными порциями - квантами. В связи с этим предположением энергия диполей также изменяется скачком от E1 до Е2. Однако мы приведем более простой вывод, принадлежащий А.Эйнштейну. Основная идея этого вывода состоит в том, что кроме спонтанных актов излучения, происходящих с вероятностью А i k существуют вынуженные элементарные акты излучения и поглощения под действием внеш-ней периодической силы, вероятности которых Вi k или Вk i , в зависимости от направления перехода.
Рассмотрим систему, состоящую из большого числа (No) диполей, находящуюся в сос-тоянии равновесия с тепловым излучением, спектральная плотность энергии которого( т.е. излучательная способность) равна en,Т .
Обозначим энергию диполя до момента излучения через E1, a энергию диполей после излучения – E2 ; число диполей в состояниях е1 и Е2 - через N1и N2 . Количество спонтанных переходов из состояния с энергией е1 в состояние с энергией Е2 равно D 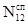 = A12 N1 .B то же время под действием теплового излучения, характеризующегося излучательной способ-ностью en,Т происходят вынужденные переходы как из состояния 1 в состояние 2, так и обратно.Число этих переходов равно D
= A12 N1 .B то же время под действием теплового излучения, характеризующегося излучательной способ-ностью en,Т происходят вынужденные переходы как из состояния 1 в состояние 2, так и обратно.Число этих переходов равно D 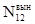 = n1В12 en,Т , D
= n1В12 en,Т , D  = N2 B21en,Т .
= N2 B21en,Т .
В состоянии теплового равновесия число переходов из состояния I в состояние 2 должно равняться числу переходов из состояния 2 в состояние l.Ha основании этого запишем D 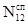 + D
+ D 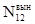 = D
= D  или А12N1 +n1В12 en,Т = N2 B21en,Т .
или А12N1 +n1В12 en,Т = N2 B21en,Т .
Отсюда находим en,Т :
en,Т = 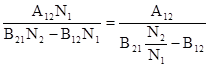 .
.
Для оценки отношения N2 / n1 используем представления классической статистики, позволяющей на основании распределения Больцмана вычислить число частиц с заданной энергией:
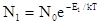 ;
; 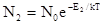 , где N0 -общее число частиц в системе. Отсюда
, где N0 -общее число частиц в системе. Отсюда
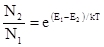 .
.
Тогда с учетом того, что, как показывает эксперимент,В12 =В 21 , получим
en,Т = 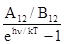 .
.
В последнем выражении использовано представление Планка, что E1 –E2 = hn. Отношение A12 / B12 не может быть вычислено в нашем курсе. Строгий расчет показывает, что оно рав-но hn3 /с2 , где с – скорость света. Поэтому выражение для излучательной способности при-обретает следующий вид:
en,Т = 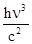
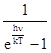 .
.
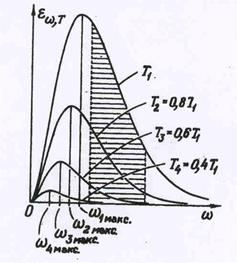 Рис.61 Зависимость излучатель-
ной спосбности от частоты и
температуры.
Рис.61 Зависимость излучатель-
ной спосбности от частоты и
температуры.
| Графическая зависимость излучательной способности приведена на рис.61, где по оси частот отложена угло-вая частота w =2nn.
§ 13-3 Законы Стефана- Больцмана и Вина.
Из рис.61 видно, что для каждой температуры излучательная способность имеет максимальное значение при определенной частоте излучения. Для определения этой частоты проведем исследова-ние на экстремум величины en,Т , предварительно проведя замену перемен-ной в целях сокращения записи. Введем новую переменную х:
х = 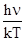 ;
тогда n = ;
тогда n = 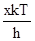 ; n3 = ; n3 = 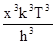 и dn = и dn = 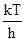 dx .
Теперь выражение для излучательной способности приобретает такой вид: dx .
Теперь выражение для излучательной способности приобретает такой вид:
|
en,Т = 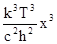
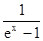 .
.
Вычисляя первую производную и сокращая полученный результат на постоянную величи-ну, имеем:
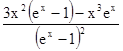 = 0.
= 0.
Из этого выражения видно, что оно равно нулю, если числитель дроби равен нулю, откуда для определения экстремального значения х получаем трансцендентное уравнение:
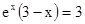 .
.
Можно показать,что это уравнение имеет решение (приближенное значение х м =2,8214 ), для простоты обозначим его а',т.е. х М = а', или hnМ / kT = а', откуда следуетзакон Вина:
nМ =аТ.
В этом выражении постоянная а является комбинацией других постоянных: а = a’ , k / h .
Определим интегральную излучательную способность Ет (она называется энергети-ческой светимостью) как еT = 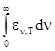 , или в обозначениях новой переменной:
, или в обозначениях новой переменной:
ET = 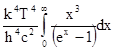 .
.
Интеграл в этом выражении является табличным,его величина равна л4 / 15.0бозначая через s комбинацию постоянных 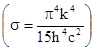 получаем следующее выражение для энергети-ческой светимости: ЕТ = sТ4, которое известно как законСтефана-Больцмана.
получаем следующее выражение для энергети-ческой светимости: ЕТ = sТ4, которое известно как законСтефана-Больцмана.
Сравним теоретические выводы с практикой.Экспериментальные данные показывают, .что при комнатной температуре максимум излучения лежит в далекой инфракрасной об-ласти, излучение в видимой области практически отсутствует. При температуре, приближающейся к 1000 К, максимум по-прежнему в инфракрасной области, однако и из-лучение в видимой части спектра становится заметным ( см.рис.61). В силу того, что интен-сивность от длинных, красных волн, к коротким, фио-летовым, падает, наибольшая интен-сивность излучения приходится на красную часть спектра - это температура «красного каления». По мере роста температуры различие в интенсивностях падает, излучение приоб-ретает желтый, а затем белый цвет. При температуре между 5000 и 6000° К максимум про-ходит через область спектра, к которой человеческий глаз наиболее чувствителен. Тем-пературе 5900 К отвечает температура поверхности Солнца, лучеиспускательная способ-ность которого близка к лучеиспускательной способности абсолютно черного тела. Такое излучение воспринимается глазом как белый, дневной свет. При более высоких темпера-турах максимум смещается в ультрафиолетовую область, а интенсивность в фиолетово - голубой области становится большей, чем в красной. Излучение приобретает голубой отте-нок.
Дата добавления: 2015-08-08; просмотров: 954;
