О П Т И К А
Лекция 10 Представления о свете.
§ !0 –1 Развитие представлений о свете.
Хотя попытки дать объяснения природы света были сделаны еще в древности (Евклид и Лукреций Кар), первая стройная теория света была разработа И.Ньютоном в кон-це семнадца-того века. Ньютон считал, что свет – это поток мельчайших частиц – корпус-кул, поэтому его теория получила название корпускулярной. Одновременно с ним Гук и Гюйгенс развивали волновую теорию, однако она не получила широкого признания отчасти из-за высокого авторитета Ньютона и отчасти из-за недостатков самой теории. которая представляла свет как упругие колебания среды Ньютон установил, что свет в представле-ниях волновой теории должен быть поперечными колебаниями, что казалось маловероят-ным, учитывая эмпирические факты распространение света в воздухе и,особенно, в меж-звездном пространстве.Лишь позднее была предложена гипотеза о существовании особой среды,заполняющей всю Вселенную,- эфира, упругие свойства которого обеспечивали тре-буемую скорость распространения света.Успехи волновой теории связаны с работами Юн-га, Френеля и Пуассона, которые были выполнены в первой половине XIX века. Работы этих исследователей позволили объяснить такие явления как интерференция и дифракция света. Д.Максвелл установил, что свет – это электромагнитные волны. В тот момент, когда волновая теория стала общепризнанной, были установлены закономерности излучения света атомами и открыт фотоэффект. Эти факты противоречили волновой теории. Позднее была развита новая теория – дуалистическая, где свету приписывались и волновые и кор-пускулярные свойства. Луи де Бройль высказал гипотезу о всеобщем дуализме материи: каждая частица обладает волновыми свойствами, и каждой волне могут быть приписаны определенная масса и импульс. Свет – лишь пример проявления дуализма в природе. В нашем курсе мы будем рассматривать преимущественно волновые явления.
§ !0 –2 Законы отражения и преломления света.
Волновая теория широко использует принцип Гюйгенса: каждая точка среды, до которой дошел волновой фронт, становится источником вторичных колебаний так, что положение волнового фронта в любой последующий промежуток времени находится как огибающая этих вторичных возбуждений. Отметим, что волновым фронтом называется поверхность, соединяющая точки,колебания в которых имеют одинаковые фазы.
    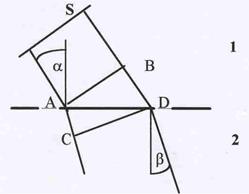 Рис.38. К выводу закона прелом-
ления света. Рис.38. К выводу закона прелом-
ления света.
| На рис.38 это изображается линией S. Руководствуясь этим принципом, выведем законы преломления и от-ражения света.Пусть на границу раздела двух сред па-дает плоский волновой фронт АВ.В момент, когда его левый край достигнет точки А (см. рис.38), в среде 2 вокруг этой точки начнет образовываться сферичес-кая волна. Правый край фронта подойдет к границе раздела через время t =BD/c, где с – скорость распро-странения света в среде1. За это время сферическая волна из точки А успеет распространиться на рассто-яние АС=vt (v –скорость распространения света в среде 2).Из рис.видно,что BAD = a и АDC = b |
как углы с взаимно перпендикулярными сторонами. Поэтому можно записать:
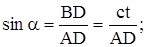
 .
.
Сравнивая эти два выражения, можно заметить, что
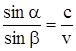 .
.
Как уже упоминалось,скорость электромагнитных волн в среде v =c/ 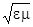 = c/n .Поэтому отношение синусов можно приравнять к показателю преломления второй среды относи-тельно первой:
= c/n .Поэтому отношение синусов можно приравнять к показателю преломления второй среды относи-тельно первой:
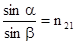 .
.
Если свет распространяется в обратном направлении, т.е из среды 2 в среду 1, то закон преломления остается в силе, но теперь n12 – это показатель преломления среды 1 относи-тельно среды 2. Можно заметить, что в этом случае угол преломления становится больше угла падения, но существует предельное значение угла преломления, т.к. синус не может быть больше единицы. Угол падения, который соответствует этому углу преломления назы-вается предельным. При дальнейшем увеличении угла падения свет не проходит в среду 1, испытывая полное внутреннее отражение.
    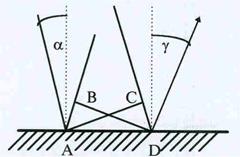 Рис.39. К выводу закона отраже-
ния света.
Рис.39. К выводу закона отраже-
ния света.
| Вывод закона отражения света производится анало- гичным способом, с той разницей, что теперь вторич-ная волна распространяется в той же среде (рис.39). Треугольники D ACD и DABD равны, т.к. сторона AD - общая, а АВ = СD =ct, где как и прежде t – вре-мя распространения волнового фронта от точки С до точки D. Из равенства треугольников следует, что CAD = ABD, как углы с взаимно перпендикулярны-ми сторонами, но CAD = a и ABD = g и a=g, т.е. угол падения равен углу отражения. |
§ !0 –3 Явление интерференции.
Интерференцией называется сложение волн от двух или нескольких источников, когда в результате сложения нарущается принцип суперпозиции интенсивностей. Как сле-дует из прошлых лекций, плотности энергии электрического и магнитного полей пропор-циональны квадратамвеличин Е и В, поэтому можно считать, что плотность энергии в элек-тромагнитной волне также пропорциональна квадрату амплитуды волны. Принято считать, что плотность энергии определяет интенсивность световой волны, которую человеческий глаз оценивает как освещенность. При сложении волн должен выполняться принцип супер-позиции энергий каждой из слагаемых волн. Наша повседневная практика дает примеры справедливости этого положения: две лампы дают в два раза больше света, чем одна. Можно показать, однако, что этот принцип выполняется не всегда.
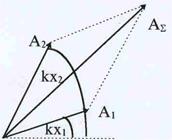 Рис.40. Сложение коге-
рентных колебаний.
Рис.40. Сложение коге-
рентных колебаний.
| Пусть имеется две плоских волны y1 = A1sin(wt –kx1) и y2 =
=A2sin(wt –kx2), где х1 и х2 -расстояния, которые прошли волны до момента встречи. Для того, чтобы найти сумму колебаний от двух волн в точке встречи, представленных в векторном виде (рис.40). Как видно из рис., по теореме косинусов можно запи-сать
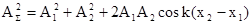 ,
т.е. результат сложения зависит от разности х2 – х1. При условии k(x2 –x1) =2pn ( n = 0,1,2 и т.д.) ,
т.е. результат сложения зависит от разности х2 – х1. При условии k(x2 –x1) =2pn ( n = 0,1,2 и т.д.)
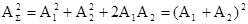 , ,
|
а при k(x2 –x1) =(2n-1) p
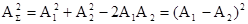 .
.
Очевидно, что при условии А1=А2 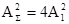 или
или 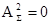 в зависимости от разности хода x2 –x1. Если учесть, что энергия каждой волны равна А2, суммарная энергия должна равняться 2А2, тогда как результат сложения либо в два раза больше, чем суммарная энергия, либо равен нулю, т.е. кажется, что не выполняется закон сохранения энергии. Колебания, для которых подобные результаты имеют место, называются когерентными. Если принцип суперпозиции выполняется, то источники называют некогерентными. Для того, чтобы волны давали когерентные колебания, необходимо выполнение трех условий:
в зависимости от разности хода x2 –x1. Если учесть, что энергия каждой волны равна А2, суммарная энергия должна равняться 2А2, тогда как результат сложения либо в два раза больше, чем суммарная энергия, либо равен нулю, т.е. кажется, что не выполняется закон сохранения энергии. Колебания, для которых подобные результаты имеют место, называются когерентными. Если принцип суперпозиции выполняется, то источники называют некогерентными. Для того, чтобы волны давали когерентные колебания, необходимо выполнение трех условий:
1.должны иметь одинаковую частоту,
2. разность фаз колебаний должна быть постоянной хотя бы на время волны наблюдений,
3. колебания каждой из суммируемых волн должны лежать в одной плоскости.
Практическое получение когерентных колебаний связано с определенными трудностями. Необходимо иметь в виду, что световые волны получаются при излучении атомов, когда электорны переходят с одного энергетического уровня на другой. Время излучения крайне незначительно и составляет около 10 –8 сек. Новый кат излучения происходит с другой на-чальной фазой, которая раз от раза изменяется случайным образом. На языке корпускуляр-
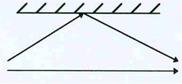 Рис.41. Схема получения
когерентных волн.
Рис.41. Схема получения
когерентных волн.
| ных представлений такая порция излучения называется кван-том, а в волновой теории ее называют цугом. Для получения когерентных волн необходимо, чтобы они происходили из одного цуга. Это можно сделать лишь путем его деления (см. рис.41). Для этих целей используются специальные приспособ-ления: билинзы Бийе, бипризмы и бизеркала Френеля и др. (рис.42). Во всех случаях явление интерференции возможно, |
если максимальная разность хода не превышает длину цуга L = ct, где t = 10 –8 сек – время излучения цуга,т.е. L=3м.
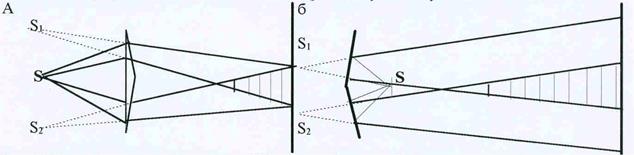 Рис.42. Интерференционные схемы: а)бипризма Френеля, б)билинза Френеля.
Рис.42. Интерференционные схемы: а)бипризма Френеля, б)билинза Френеля.
|
«Раздвоение» источника достигается либо преломлением в призме, либо отражением в двух зеркалах. Угол «разворота» зеркал и преломляющий угол призмы близки к 1800 для того, чтобы достичь наилучшей видимости картины интерференции.
Как было показано, амплитуда суммарных колебаний определяется разностью хода интер-ферирующих волн или разностью фаз складывающихся колебаний. Если разность фаз Dj изменяется случайным образом, то среднее значение cosDj за время наблюдения равно ну-лю, и мы видим обыкновенное сложение интенсивностей. Если же источники когерентны, то при условии k(x2 –x1) = 2pn колебания дадут максимум суммарной амплитуды, а при k(x2 –x1) = (2n-1)p - минимум. Учитывая, что k = 2p/l , ( l - длина волны ) условия макси-мума и минимума интенсивностей можно записать так:
(x2 –x1) = 2nl/2 для максимума и
(x2 –x1) = (2n-1)l/2 для минимума.
Это значит, что если разность хода интерферирующих волн равна четному числу полуволн, то получается максимум, а если нечетному – минимум интенсивности. Нарушение закона сохранения энергии при этом не происходит. Она лишь перераспределяется – в max – боль-ше, а в min меньше, но средняя энергия остается неизменной. Глаз воспринимает такое перераспределение как чередование темных и светлых полос, контрастность которых определяется соотношением интенсивностей интерферирующих источников.
§ !0 –4 Полосы равной толщины.
Наиболее часто в повседневной жизни явление интерференции проявляется в так называемых полосах равной толщины, которые получаются при отражении света от тонких
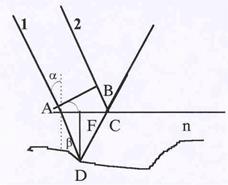 Рис.43. Интерференция в тон-
ких пленках.
Рис.43. Интерференция в тон-
ких пленках.
| пленок. Пусть имеется тонкая пленка переменной тол-щины (рис.43), на которую падают параллельные лучи света. Выберем два луча, один из которых отражается от верхней поверхности пленки, а другой – от нижней. Раз-ность хода между лучами определяется удвоенной длиной AD и участком ВС. Однако следует иметь в виду, что пленка является более плотной оптической средой, и ско-рость света в ней меньше. Вследствие этого время, затра-чиваемое светом на прохождение пути AD будет больше в n раз, где n – показатель преломления пленки. Поэтому принято говорить об оптической длине пути света, кото-рая равна ADn. Теперь разность оптических путей лучей |
1 и 2 D = 2n(AD) – BC +l/2. Величина l/2 добавляется потому, что происходит изменение фазы волны на 180 0, что эквивалентно увеличению пути на l/2.Из рис можно увидить, что AD = DF/cosb;AF = DFtgb;AC = 2AF= =2DFtgb;BC =ACsina = 2DFtgb sina. Согласно закону преломления света sina = nsinb. C учетом этого D= 2nDF/cosb - 2DFsinatgb + +l/2 = 2nDF(1- -sin2b)/cosb +l/2 = 2DFcosb +l/2.
Если D= (2n-1)l/2, то 2DFncosb =nl cоответствует условию минимума освещенности, а D= =nl= 2DFncosb +l/2 – условию максимума.Условия интерференции будут одинаковыми для всех мест, где толщина пленки также одинакова, в связи с чем говорят, что интерференци-онная картина локализована на поверхности пленки. При наблюдении в белом свете карти-на усложняется, т.к. для каждого из цветовых компонент белого света условия max и min будут свои. На поверхности пленки будут видны цветные пятна (вспомните пленки бензи-на и масла на поверхности луж). Частным случаем полос равной толщины являются
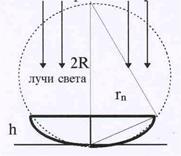 Рис.44. Схема для наблю-
дения колец Ньютона.
Рис.44. Схема для наблю-
дения колец Ньютона.
| кольца Ньютона. Роль пленки переменной толщины здесь иг-рает воздушная прослойка между собирающей линзой и стек-лянной пластинкой (см.рис.44). Т.к. оптическая структура об-ладает осевой симметрией, наблюдающиеся интерференци-онные полосы принимают вид концентрических колец. Для толщины прослойки h разность хода между лучами, отражен-ными от нижней поверхности линзы и от пластинки соот-ветственно равна D =2h +l/2 - (l/2) добавляется из-за условий отражения. В то же время из рис.44 на основании свойств перпендикуляра. опущенного из вершины прямого угла на ги-потенузу, следует: |
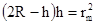 ,
,
где m – номер наблюдаеиого кольца. Пренебрегая малой величиной h2 по сравнению с ра-диусом линзы R,находим 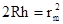 . Для темных колец D = (2m+1)l/2 = 2h + l/2 и 2h =ml. Подставляя это соотношение в формулу для квадрата радиуса кольца, получим:
. Для темных колец D = (2m+1)l/2 = 2h + l/2 и 2h =ml. Подставляя это соотношение в формулу для квадрата радиуса кольца, получим:
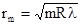 .
.
Лекция 11 Дифракция света.
§ 11 –1Метод зон Френеля.
Дифракией называется когерентное рассеяние света на объектах, геометрические размеры которых сранимы с длиной световой волны. Наблюдающаяся дифракционная кар-тина является результатом интерференции вторичных источников, образующихся на по-верхности объекта. Расчет интерференционной картины можно проводить пользуясь мето-дом суперпозиции, однако применение этого метода сопряжено с известными математи-ческими трудностями. В связи мы ограничимся рассмотрения качественного подхода к ре-шению поставленной задачи, развитого Френелем. Основной идеей, определяющей сущ-ность такого рассмотрения, является принцип Гюйгенса –Френеля, который представляет собой дополненный принцип Гюйгенса. Френель постулировал, что все элементарные вто-ричные источники являются когерентнми. Для оценки результирующей амплитуды колебаний в точке наблюдения был разработан специальный метод, получивший название метода зон Френеля. Согласно этому методу волновой фронт (будем называть волновым фронтом поверхность, которая соединяет все точки, колеблющиеся в одинаковой фазе) раз-бивается на отдельные участки, именуемые зонами. Разбиение на зоны должно удовлетво-рять двум условиям:
1.площади всех зон одинаковы,
2.расстояния от двух соседних зон до точки наблюдения отличаются на половину длины волны.
Первое условие означает, что амплитуды колебаний от всех зон в точке наблюдения будут одинаковыми, тогда как из второго условия следует, что колебания двух соседних зон скла-дываются в противофазе. В этом случае вместо вычисления сложных интегралов достаточ-но подсчитать число зон. Если оно – четно – в точке наблюдения будет минимум освещен-ности (зоны попарно гасят друг друга), если же количество зон на участке волнового фрон-та, видимого из точки наблюдения, окажется нечетным – в ней будет конечная освещен-ность.
§ 11 –2 Метод векторных диаграмм.
Для оценки вкладов от каждой зоны в суммарную освещенность используем метод векторных диаграмм. Для этого разобьем каждую зону на ряд узких «подзон» так, что каж-дая подзона отличается от соседней лишь небольшим сдигом по фазе. Колебания каждой из «подзон» будем представлять в виде вектора, длина которого определяется амплитудой ко-
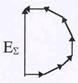 Рис.45. Векторная
диаграмма одной
зоны.
Рис.45. Векторная
диаграмма одной
зоны.
| лебаний. Площади «подзон» выберем одинаковыми. Как видно из рис.45, вектора каждой «подзоны» оказываются повернутыми отно-сительно соседних на небоьшой угол, но «подзоны» на противополож-ных краях зоны отличаются по фазе на 1800 .Суммарное действие всех «подзон» изображается вектором ЕS . Нетрудно сообразить, что при устремлении ширины каждой «подзоны» к нулю, получившаяся лома-ная линия превращается в плавную полуокружность. |
Действие двух зон должно быть равным нулю, но оказывается, что амплитуды колебаний зон не совсем одтнаковые. Их величина зависит от косинуса угла между нормалью к по-верхности зоны и направлением на точку наблюдения. Результат сложения двух и трех зон
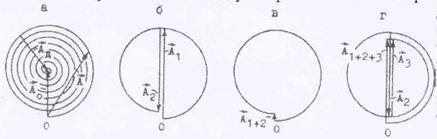 Рис.46. Векторные диаграммы для разного числа зон.
Рис.46. Векторные диаграммы для разного числа зон.
| показан на рис.46( б,в и г). Как видно из рис., две зо-ны почти уничтожаются, а амплитуда третьей зоны почти равна амплитуде первой. Там же показано (рис.46а) действие всего волнового фронта А0, ког-да препятствие отсутству- |
ет. Оно оказывается в два раза меньше, чем действие первой зоны. Витки спирали располо-жены достаточно плотно, и при большом количестве открытыз зон суммарная амплитуда АS » А0 остается практически неизменной при изменении числа зон.
§ 11 –3 Дифракция Френеля на круглом отверстии.
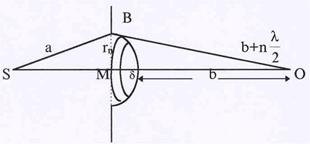 Рис.47. К вычислению радиуса зоны.
Рис.47. К вычислению радиуса зоны.
| Применим метод зон к анализу так называе-мой дифракции Френеля, когда источник света – точечный, и волновая поверхность имеет форму сферы.В качестве препятствия рассмотрим небольшое круглое отверстие в непрозрачном экране. выберем точку наблю-дения О так, чтобы в отверстии укладыва-лось бы целое число зон Френеля. Пусть волновой фронт от точечного источника S, |
дошедший до экрана, имеет радиус SB = а (см. рис.47). Расстояние от точки наблюдения О до плоскости экрана равно МО = b+d. Мысленно разобьем волновой фронт на концентри-ческие зоны ( на рис.47 показана одна зона) так, что расстояние от n – зоны до точки наблю-дения О равно b + nl/2. Из треугольника SBM по теореме Пифагора получим:
МВ2 = SB2 – SM2 = 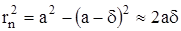 . (IV)
. (IV)
Аналогично из DОМВ : 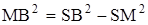 =
= 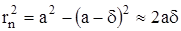 . (V)
. (V)
Члены, содержащие множители l2 и d2, отброшены как малые по сравнению с a и b. При-равнивая правые части уравнений (IV) и (V), получим 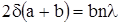 Выражая отсюда d и подставляя его в (IV), получим формулу для радиуса любой зоны:
Выражая отсюда d и подставляя его в (IV), получим формулу для радиуса любой зоны:
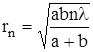 .
.
Численные значения радиуса первой зоны можно оценить, полагая a » b ~ 1м, l » 0,5мкм. Подстановка этих значений показывает, что r1 »0,3 мм. Поэтому при диаметре отверстия 1 - -2 мм в нем уложится 5-7 зон. Поскольку их амплитуды примерно одинаковы, результат сложения существенно зависит от числа зон. При нечетном числе зон в точке наблюдения
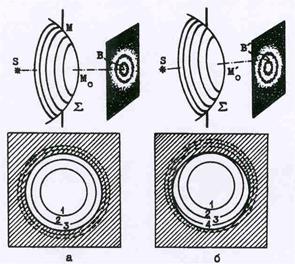 Рис.48. Смещение зон относительно отверстия.
Рис.48. Смещение зон относительно отверстия.
| будет максимум, а при четном – минимум ос-вещенности. Рассмотрим, как будет изменять-ся результат сложения колебаний при измене-нии положения точки О. Если точка смещается вдоль оси SO, то характер разбиения на зоны не изменится, произойдет лишь изменение числа зон, укладывающихся в отверстии, т.е. будет наблюдаться чередование максимумом и минимумов освещенности. Если же точка О смещается перпендикулярно оси SO, то харак- тер разбиения на зоны также не изменится, но произойдет поворот направления наблюдения относительно перпендикуляра, восставленного из центра отверстия к плоскости экрана (см. рис. 48. Вследствие этого часть зон начнет за-крываться, что приведет к изменению осве-щенности. Пусть для определенности в тот мо- |
мент, когда точка наблюдения находится на оси OS, а в отверстии укладывается нечетное число зон (например – три). Когда часть наружной зоны начнет закрываться, освещенность уменьшится.Одновременно с противоположного края отверстия появится часть новой зоны, которая еще больше уменьшит освещенность ( здесь нада вспомнить, что соседние зоны гасят друг друга). Поэтому при дальнейшем удалении точки наблюдения от оси наступит момент, когда освещенность уменьшится до нуля..Это условие будет выполняться для всех точек, находящихся на окружности, радиус которой определяется расстоянием от точки на-блюдения до оси OS. Вокруг светлой точки появится темное кольцо, продолжая рассужде-ния подобным образом, можно придти к заключению, что дифракционная картина от круг-лого отверстия пред-ставляет собой чередование чветлых и темных колец.
§ 11 –4 Дифракция Френеля на круглом экране.
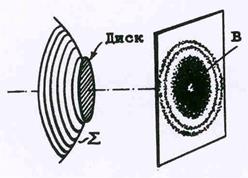 Рис.49. Диффракция на круглом
экране.
Рис.49. Диффракция на круглом
экране.
| Пусть препятствием служит теперь небольшой не-прозрачный диск, и пусть радиус волнового фронта настолько велик, что волновая поверхностьS прак-тически совпадает с плоской поверхностью диска ( рис.49). Разобьем волновой фронт на зоны спосо-бом, аналогичным изложенному в предыдущем па-раграфе. В точку наблюдения В приходят все коле-бания волнового фронта за исключением тех зон, которые закрыты диском. Это суммарное колебание на векторной диаграмме (см. рис.46) изобразится вектором АД . Начало вектора соответствует точке, лежащей на краю диска. При изменении расстоя- |
ния от диска до точки В число закрытых зон будет меняться, и начало вектора АД станет описывать окружность вокруг центра спирали, тогда как конец вектора всегда находится в ее центре. При большом числе открытых зон длина вектора почти не изменяется. Поэтому в точке В будет наблюдаться светлое пятно (пятно Пуассона).
§ 11 –5 Дифракция Фраунгофера.
Этот вид дифракции наблюдается в параллельных лучах, когда волновой фронт ста-новится плоским, а зоны Френеля принимают вид узких прямоугольных полосок. Опти-
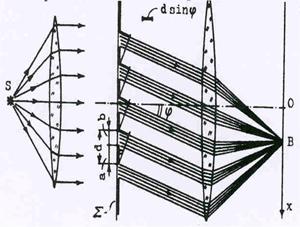 Рис.50. Диффракция Фраунгофера на
щели.
Рис.50. Диффракция Фраунгофера на
щели.
| ческая схема наблюдения этого вида диф-ракции представлена на рис.50. В роли пре-пятствия здесь выступает узкая прямоуголь-ная щель (узкая сторона щели лежит в плос-кости рисунка). Разбиение поверхности щели на зоны Френеля осуществляется следующим образом: через край щели (точка М0 ) прово-дится плоскость (М0 Р), перпендикулярная идущим в точку наблюдения лучам, а затем проводятся параллельные ей плоскости, от-стоящие друг от друга на полволны.Эти плос-кости, пересекая плоскость щели, разбивают ее на зоны Френеля, которые представляют собой полосы, параллельные краям щели: |
границы зон изображаются точками М 0,М1, М2 …, а отрезки М 0М1 , М1М2 определяют ширину первой, второй и т.д.зон.Из рис видно,что в расчете не учитывается разность хода от плоскости М0Р до фокуса линзы Л, предназначенной для создания резкого изображения на экране. Это является следствием таутохронизма линзы, означающего, что лучи прохо-дят пути от М0Р до фокуса линзы за одинаковое время. Попутно заметим, что линза ЛК предназначена для создания параллельного пучка лучей. Предположим, что угол j выбран таким образом, что на ширине щели укладывается целое число зон, т.е. МР = kl/2 ( k = 1,2,3 …). В то же время из DМ0РМ следует, что МР = ММ0 sin j или MP = bsinj. Если число зон четное ( k =2m), то выбранное направление соответствует минимуму освещенности ( зоны попарно гасят друг друга), а если – нечетно (k = 2m-1) – то максимуму. Таким образом, имеем:
bsinj = ml - условие минимума,
bsinj = (2ь-1)l/2 – условие максимума.
При движении точки наблюдения в направлении, перпендикулярном плоскости рисунка (вдоль длинной стороны щели) картина не изменяется, и на экране видны чере-дующиеся темные и светлые полосы. Однако интенсивности светлых полос быстро убы-вают так, что практически с трудом удается наблюдать более двух таких полос с каждой стороны от центрального максимума.
§ 11 –6 Дифракционная решетка.
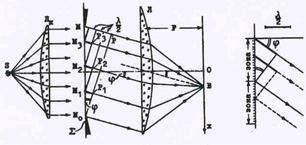 Рис.51. Дифракция на щели.
Рис.51. Дифракция на щели.
| Возьмем теперь в качестве препятствия диф-ракционную решетку, т.е непрозрачную пла-стинку с одинаковыми параллельнымии рав-ноотстоящими друг от друга щелями(рис51). Обозначим, как и прежде, ширину щели b, а ширину непрозрачного участка – а . Величи-ну d = а + b назовем периодом или постоян-ной решетки.Выбирая ту же волновую по-верхность, что и при рассмотрении дифрак- |
ции на одной щели, и применяя принцип Гюйгенса-Френеля, можно заметить, что теперь в каждой точке экрана для наблюдений собираются лучи, идущие от всех N щелей. Для вы-числения результата сложения выделим в каждой щели одинаковые точки(например- верх-ние).Две таких точки в соседних щелях при заданном угле j имеют разность фаз, равную
q = 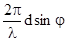 . В точке наблюдения колебания от всех щелей сложатся в одинаковых фазах, если разность фаз q равна 2pn (n =0,1,2…), т.е. q =
. В точке наблюдения колебания от всех щелей сложатся в одинаковых фазах, если разность фаз q равна 2pn (n =0,1,2…), т.е. q = 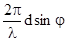 = 2pn, откуда получается ус-ловие для максимумов dsinj = nl . Можно показать, что кроме этих максимумов существу-ют еще другие, положения которых зависит от числа щелей, но интенсивность их крайне не значительна. Чтобы различать эти максимумы с теми, которые удовлетворяют условию dsinj = nl, принято называть их дополнительными максимумами, а максимумы, соответ-ствующие условию dsinj = nl - главными. Значение числа n определяет порядок главного максимума (первый максимум, второй и т.д) Между максимумами должны располагаться минимумы освещенности, но с практической точки зрения они не представляют особого интереса и в нашем курсе не рассматриваются.
= 2pn, откуда получается ус-ловие для максимумов dsinj = nl . Можно показать, что кроме этих максимумов существу-ют еще другие, положения которых зависит от числа щелей, но интенсивность их крайне не значительна. Чтобы различать эти максимумы с теми, которые удовлетворяют условию dsinj = nl, принято называть их дополнительными максимумами, а максимумы, соответ-ствующие условию dsinj = nl - главными. Значение числа n определяет порядок главного максимума (первый максимум, второй и т.д) Между максимумами должны располагаться минимумы освещенности, но с практической точки зрения они не представляют особого интереса и в нашем курсе не рассматриваются.
Полученные условия главных максимумов справедливы для одной длины волны све-та. Если же свет – белый, то для каждого из его составляющих цветов условия максимумов будут соответствовать различным углам j, т.е. на экране получится набор цветных полос. Другими словами, дифракционная решетка позволяет анализировать спектральный состав световых лучей. Поэтому решетку можно использовать как спектральный аппарат. Все спектральные аппараты характеризуются такими величинами как дисперсионная область, угловая дисперсия и разрешающая способность.
Дисперсионная область G определяет ширину спектрального интервала отl доl+ Dl, в котором максимумы для различных волн не перекрываются друг с другом.Величина G =l/n, где n - порядок максимума.
Угловая дисперсия D определяет угловое расстояние между волнами, длина которых отличается на единицу (длины).Выражение для определения D можно получить, дифферен-цируя условия главных максимумов: dcosj =lnd. Отсюда D определяется как
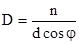 .
.
Под разрешающей способностью А подразумевается возможность спектрального аппарата различать линии, соответствующие близким значениям длин волн l и l + dl. Она определяется выражением
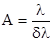 .
.
§ 11 –7 Дифракция рентгеновских лучей.
Рентгеновскими лучами называют электромагнитное излучение, длина волн которого примерно равна !0 –10 м. Длина волны рентгеновских лучей много меньше световых волн,
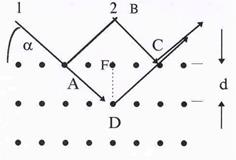 Рис.52. Дифракция рентгенов-
ских лучей.
Рис.52. Дифракция рентгенов-
ских лучей.
| поэтому наблюдать дифракцию этих лучей в стандар-тных схемах не удается. Препятствиями, размеры кото-рых сравнимы с длиной волны рентгеновских лучей, могут служить лишь межатомные расстояния в твер-дых телах. Схема дифракции показана на рис.52. Ато-мы кристалла расположены в правильном порядке, об-разуя плоскости, отражающие лучи. Коэффициент пре-ломления лучей близок к единице, и лучи отражаются от различных плоскостей без заметного преломления (nр » 1). Обозначая угол скольжения лучей через a, а расстояние между отдельными слоями через d, можно |
заметить, что разность хода между интерферирующими лучами d =AD +DC – BC. Из DADF AD = FD/sina; AF = dtga, а из DАВС ВС = 2AFcosa. С учетом того, что AD = DC, имеем:
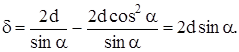
Условие максимума будет выполняться при 2dsina = kl , где k –целое число. Полученная формула носит название формулы Вульфа – Брэггов.
Рассмотренный случай дифракции относится к конкретным межатомным плоскостям и монохроматическому излучению, что заметно упрощает анализ условий образования мак-симумов. В действительности же межатомные плоскости могут быть ориентированы произ- вольным образом, причем в роли интерферирующих лучей могут выступать лучи, отраженные не только от соседних плоскостей. Кроме того, следует иметь ввиду, что реаль-ные кристаллические структуры имют три измерения, каждому из которых могут соответст-вовать различные условия образования максимумов. Тем не менее рентгенографический метод анализа кристаллов нашел широкое применение в петрографии, рентгеноструктур-ном анализе и ряде других приложений.
Лекция 12 Поляризация света. Взаимодествие света с веществом.
§12-1 Явление поляризации.
Обычно считается, чтопонятие поляризации связано с сохранением неизменной ориен-тации плоскости колебаний. Говорить о поляризации имеет смысл только для поперечных колебаний. Свет, как мы знаем, является электромагнитной волной, а эти волны – попереч-ны и поляризованы (см.рис.37) так, что казалось бы, световые колебания всегда должны быть поляризованы. Однако мы знаем, что световые волны испускаются отдельными цуга-ми, продолжительность которых не превышает 10–8 сек. Процесс испускания является слу-
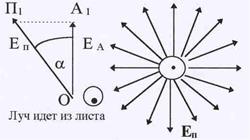 Рис.53. Прохождение света через
анализатор и поляризатор. Рис.53. Прохождение света через
анализатор и поляризатор.
| чайным, и фаза испущенной волны, а также ориента-ции векторов Е и В в плоскости, пер пендикулярной направлению излучения, могут быть любыми.Т.к. вектора Е и В в волне жестко связаны друг с другом, имеет смысл рассматривать лишь один из них (пусть, для определенности, это будет вектор Е). В среднем, в любой волне все допустимые ориентации вектора Е равновероятны (см. рис.53). Существуют приспобле-ния, называемые поляризаторами, которые обладают способностью пропускать через себя световые лучи |
только с одним направлением плоскости колебаний электрического вектора Е, так что на выходе поляризатора свет становится плоско (линейно) поляризованным. Человеческий глаз не в состоянии обнаружить, поляризован свет или неполяризован. Для того, чтобы обнаружить это, необходимо использовать второе такое же приспособление, которое на-зывают анализатором. Если направление пропускания анализатора и поляризатора совпа-дают, луч света на выходе из анализатора имеет максимальную интенсивность. При про-извольном угле a между направлениями анализатора и поляризатора (см.рис.53) амплитуда световых колебаний, выходящих из анализатора ЕА = ЕП cosa, где ЕП – амплитуда колеба-ний на выходе из поляризатора. В электромагнитной волне плотность энергии (интенсив-ность) пропорциональна квадрату амплитуды колебаний Е, т.е. I П ~ Е 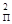 и IА ~ Е
и IА ~ Е 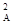 . На осно-вании этого получаем:
. На осно-вании этого получаем:
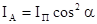 .
.
Это соотношение называется законом Малюса.
§12-2 Закон Брюстера.
Простейшим приспособлением для поляризации света может служить прозрачное диэлектрическое зеркало. Пусть на диэлектрик (см. рис.54) падает луч естественного све-
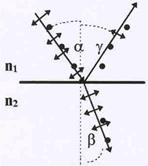 Рис.54. Поляризация света при отражении и преломлении.
Рис.54. Поляризация света при отражении и преломлении.
| та. Обозначим через n2 коэффициент преломления диэлектрика, а через n1 – коэффициент преломления среды, откуда падает свет (a - угол падения, b - угол преломления). Условимся изображать направление колебаний вектора Е в виде точек или тонких чер-точек, где точка изображает направление вектора, перпендику-лярное плоскости чертежа, а черточка означает, что вектор Е ле-жит в плоскости чертежа. В естественном свете равновероятны все направления колебаний Е, что изображается в виде того, что количество точек и черточек одинаково. Опыт показывает, что отраженный и преломленнвй лучи становятся частично поляри-зованными, причем в отраженном свете преобладающими ста-новятся колебания, плоскость которых перпендикулярна плос- |
кости чертежа, а в преломленном предпочтительнее оказываются направления колебаний в плоскости чертежа ( на рис. это изображается в виде преимущества числа точек или черто-чек). Существует угол падения, при котором отраженные лучи становятся полностью поля-ризованными. Этот угол называется углом Брюстера, его значение связано с отношением n2/n1 = n21, т.е. относительным показателем преломления:
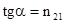 .
.
Качественное объяснение этого закона следует из рассмотрения микроскопической картины распространения светв в веществе. Рассмотрим упрощенную модель взаимодействия света с веществом, согласно которой переменное электрическое поле световой волны приводит в двихение атомы вещества. Атом же представим как диполь, где роль отрицательного заряда
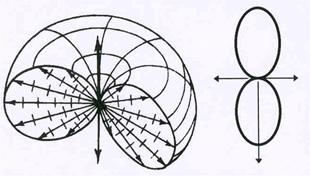 Рис.55. Индикатрисса излучения диполя.
Рис.55. Индикатрисса излучения диполя.
| играет внешний электрон, а вся остальная часть атома рассматривается как положи-тельный заряд (ион). Т.к. масса положитель-ного иона во много раз ( более 2000) больше, чем масса электрона, можно рассматривать лишь колебания электрона. Строгая теория электромагнетиза показывает, что колеблю-щийся диполь становится излучателем элек-тромагнитных волн, причем интенсивность излучения различна в разных направлениях. Для иллюстрации анизотропности излуча- |
тельной способности диполя строится диаграмма (индикатрисса), на которой интенсивность излучения в заданном направлении изображается в виде вектора. Длина этого вектора и ха-рактеризует интенсивность излучения. Пространственное изображение индикатриссы при-ведено на рис.55. В правой части рисунка показано сечение диаграммы вертикальной пло-скостью, проходящей через центр диаграммы.
Положения рассмотренной модели применим для объяснения закона Брюстера. В па-дающем на границу раздела двух сред естественном свете вектор Е принимает всевозмож-ные направления (см.рис.53), но без ограничения общности можно рассматривать лишь два:
       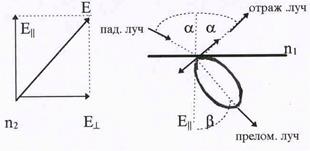
   Рис.56. К выводу закона Брюстера. Рис.56. К выводу закона Брюстера.
| Е и Е , т.к. любой вектор Е можно пред-ставить как их сумму (см. левую часть рис.56). Вектор Е соответствует колебани-ям, которые происходят в направлении, пер-пендикулярным плоскости чертежа,а Е ха-рактеризует колебания в этой плоскости. Представляет интерес рассмотреть лишь со-ставляющую Е .Если диполь излучает волну Е в направлении преломленного луча ( пра- |


 вая часть рис.56), то из диаграммы направленности следует, что в направлении,перпендику-лярном этому лучу, никакого излучения не происходит. В этом направлении излучаются лишь волны с напряженностью Е . Из этого следует, что если луч преломленный и луч от-раженный перпендикулярны друг другу, то в отраженном свете полностью отсутствуют ко-лебания с Е .Из рисунка видно, что b +a + 900 = 1800,или b+a =900, тогда как из закона преломления следует, что sina = n21 sinb . Подставляя в закон преломления b = 900 - a , по-лучим sina = n21sin(900 -a) = n21cosa, т.е.
вая часть рис.56), то из диаграммы направленности следует, что в направлении,перпендику-лярном этому лучу, никакого излучения не происходит. В этом направлении излучаются лишь волны с напряженностью Е . Из этого следует, что если луч преломленный и луч от-раженный перпендикулярны друг другу, то в отраженном свете полностью отсутствуют ко-лебания с Е .Из рисунка видно, что b +a + 900 = 1800,или b+a =900, тогда как из закона преломления следует, что sina = n21 sinb . Подставляя в закон преломления b = 900 - a , по-лучим sina = n21sin(900 -a) = n21cosa, т.е.
tga = n21.
§12-3 Поглощение света.
При прохождении света через вещество часть энергии световой волны поглощается, переходя во внутреннюю энергию вещества. Для оценки величины этих по-терь рассмотрим световой поток, распространяющейся вдоль оси х (рис.57).0пыт показы-вает,что при прохождении очень тонкого слоя вещества толщиной dx относительная убыль
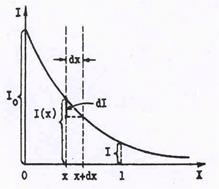 Рис.57. Изменение интенсивнос-
ти света при его поглощении.
Рис.57. Изменение интенсивнос-
ти света при его поглощении.
| интенсивности, т.е.отношение изменения интенсив-ности dIв этом слое к интенсивности падающего света I(х) ( см.рис.57),пропорциональна толщине слоя:
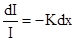 ,
где коэффициент К, зависящий от свойств вещества, называется коэффициентом поглощения.Знак минус отражает убывание интенсивности с ростом х. Измене-ние интенсивности света при прохождении слоя конеч-ной толщины х находится путем прямого интегри-рования вышеприведенной формулы: ,
где коэффициент К, зависящий от свойств вещества, называется коэффициентом поглощения.Знак минус отражает убывание интенсивности с ростом х. Измене-ние интенсивности света при прохождении слоя конеч-ной толщины х находится путем прямого интегри-рования вышеприведенной формулы:
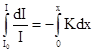 . .
|
Потенцируя последнюю формулу, получим известный закон Бугера: 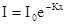 .
.
§ 12 - 4 Рассеяние света.
Плоская волна, распространяющаяся в однородной среде, остается плоской.Однако если среда неоднородна и в ней имеются включения с другими оптическими свойствами, то кроме волны, распространяющейся в первоначальном направлении, появляются волны, рассеянные в стороны. Эти волны уносят часть энергии и уменьшают интенсивность первоначального луча. Характер рассеяния зависит от размеров и природы неоднородностей.Если их размеры больше длины волны.то наблюдается чисто геометрическое рассеяние.Это касается прежде всего твердых частиц, взвешенных в воздухе.Падающий на разные участки поверхности частицы солнечный свет отражается под различными углами. Если при этом спектральный состав света не меняется, то рассеянный свет остается белым (примером это-го может служить белый цвет неба в пустынях.когда восходящие воздушные потоки пере-носят в верхние слои атмосферы мелкие частицы песка). В целом наблюдаемая картина рас-сеяния очень чувствительна к размерам и форме неоднородностей( радуга и гало вокруг солнца, вызванные наличием в земной атмосфере соответственно капелек и льдинок).
Если размеры неоднородносей существенно меньше длин волн света, то интен-сивность рассеянного света удовлетворяет закону Рэлея: Iрас~ Io w4 , где w -частота падаю-щего света, причем интенсивность рассеянного света различна по разным направлениям (т.е анизотропна). Сильная зависимость интенсивности рассеянного света от частоты означает,
 Рис.58. Рассеяние света в атмосфере.
Рис.58. Рассеяние света в атмосфере.
| что существенно сильнее рассеиваются вол-ны с большей частотой. В частности, если через среду идет волна от источника белого света (от Солнца - см.рис.58),то при наблю-дении сбоку среда кажется голубоватой, а сам источник на просвет выглядит более красным. Этим объясняется голубой цвет неба и красный цвет зари. Разные цветовые оттенки получаются из-за разных геометри- |
ческих расположении источника и наблюдателя. Так в глаз наблюдателя 1 ( см.рис.) прихо-дит прямой луч, тогда как наблюдатель 2 видит, в основном, рассеянные лучи.
§ 12 - 5 Дисперсия света.
 |
Дисперсией называется зависимость скорости распространения световой волны в среде от частоты. Поскольку скорость волны однозначно связана с показателем прелом-ления среды ( v = c/n; n =
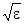 ), то нашей задачей будет выяснение характера зависимости диэлектрической постоянной от частоты. Здесь уместно напомнить, что e =1+ k (k - диэлектрическая восприимчивость, определяющая соотношение между поляризацией ве-щества Р и действующем электрическим полем Е : Р = eо kЕ ).В то же время величина вектора поляризации определялась как суммарный дипольный момент единичного объема: Р =Nqx, гдe величина qx характеризует дипольный момент каждой молекулы диэлектрика. При решении задачи будем пользоваться той же моделью.что применялась ранее при рас-смотрении закона Брюстера. Под действием переменного электрического поля световой волны расстояние электрона до положительного иона периодически изменяется.т.е. элек-трон совершает вынужденные колебания под действием внешней периодической силы.Вид этого уравнения, и его решение уже изучались ( см уравнение колебаний в кон-туре).Поэтому можно сразу написать выражение для амплитуды колебаний электрона в атоме:
), то нашей задачей будет выяснение характера зависимости диэлектрической постоянной от частоты. Здесь уместно напомнить, что e =1+ k (k - диэлектрическая восприимчивость, определяющая соотношение между поляризацией ве-щества Р и действующем электрическим полем Е : Р = eо kЕ ).В то же время величина вектора поляризации определялась как суммарный дипольный момент единичного объема: Р =Nqx, гдe величина qx характеризует дипольный момент каждой молекулы диэлектрика. При решении задачи будем пользоваться той же моделью.что применялась ранее при рас-смотрении закона Брюстера. Под действием переменного электрического поля световой волны расстояние электрона до положительного иона периодически изменяется.т.е. элек-трон совершает вынужденные колебания под действием внешней периодической силы.Вид этого уравнения, и его решение уже изучались ( см уравнение колебаний в кон-туре).Поэтому можно сразу написать выражение для амплитуды колебаний электрона в атоме:
где b характеризует затухание колебаний, а w0 может рассматриваться как собственная частота колебаний электрона в атоме.Для упрощения математических выкладок будем пренебрегать затуханием,т.е положим b = 0.Тогда величина поляризации равна:
Р = 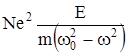 .
.
С другой стороны,выше указывалось,что Р = e0 kЕ, поэтому
k = 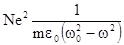 .
.
Тогда e = 1 +k = 1 + 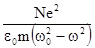 ; e = n2 .
; e = n2 .
Таким образом, имеем:
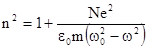 .
.
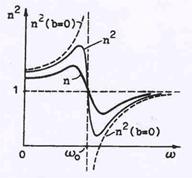 Рис.59 Частотная зависи-
мость показателя прелом-
ления.
Рис.59 Частотная зависи-
мость показателя прелом-
ления.
| График частотной зависимости в сделанных упрощениях по-казан на рис.59. Из рис. видно,что вдали от резонансной частоты показатель преломления (точнее n2 ) возрастает про-порционально квадрату частоты.Такая частотная зависимость получила название нормальной дисперсии. Когда же частота внешних колебаний приближается к частоте собственных, амплитуда возрастает неограниченно.Ясно,однако,что этот результат есть следствие наших упрощений. При наличии за-тухания кривая имеет конечный максимум ( см. рис.59 ). Вблизи резонансной кривой показатель преломления имеет другой характер зависимости. Говорят, что - это область ано-мальной дисперсии, т.к. для нее величина n2 падает с ростом частоты, причем это наблюдается на фоне повышения пог-лощения света (амплитуда колебаний электрона возрастает). |
Дата добавления: 2015-08-08; просмотров: 702;
