Колебательный контур. Излучение электромагнитных волн

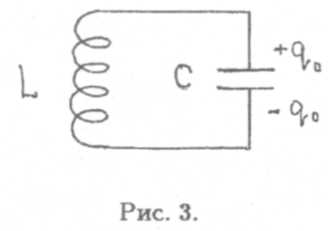
Простейший колебательный контур, в котором нет потерь на выделение тепла, показан на рис. 3.

Он состоит из конденсатора емкостью С и катушки индуктив­ности L. Пусть в момент времени t = 0 конденсатор был заряжен,

а ток в контуре отсутствовал. Тогда при t > 0 конденсатор на­чинает разряжаться через катушку индуктивности и процессы, происходящие в контуре, можно описать уравнением

Здесь мы воспользовались вторым правилом Кирхгофа и учли, что в замкнутом контуре алгебраическая сумма падений напря­жений равна алгебраической сумме эдс. Падение напряжения на обкладках конденсатора V = q/c. Учитывая формулу для э.д.с. самоиндукции, а также, что

преобразуем (11) к виду

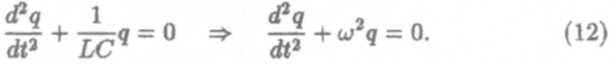
Здесь w = 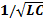. Следовательно, период колебаний T=2π/ω= 2π 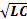.С уравнением (12)мы уже встречались много раз. Это уравнение описывает гармонические незатухающие колебания и имеет решение

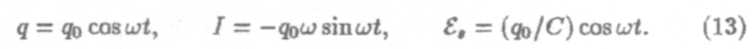
Если колебательный контур сделать открытым, то часть энер­гии будет излучаться в окружающее пространство. При этом,

чтобы поддерживать постоянную амплитуду колебаний в конту­ре, его надо подпитывать генератором электромагнитных коле­баний. Для увеличения мощности излучаемого сигнала его ча­стота должна совпадать с частотой собственных колебаний кон­тура.

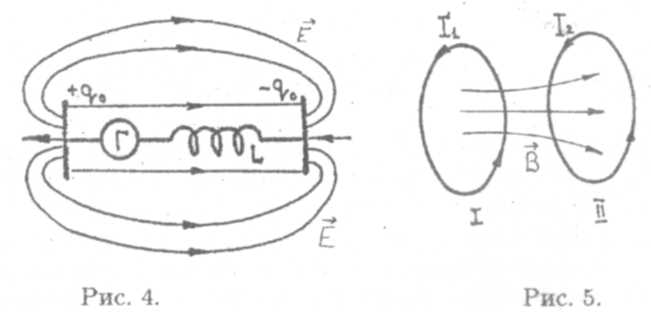
Возможная модель такой излучающей системы показана на рис. 4. Здесь Г — генератор. В пространстве вокруг контура появляется излучаемое электромагнитное поле. Чтобы не пере­гружать рисунок 4, на нем изображена только электрическая со­ставляющая этого поля.

В заключение отметим, что кроме самоиндукции имеет ме­сто также явление взаимной индукции (рис. 5). Ток в контуре I порождает магнитный поток через контур II, и наоборот

Величины L₁₂ = L₂₁ называются коэффициентами взаимной ин­дукции контуров. Изменение тока в контуре I порождает э.д.с. в контуре II. Очевидно

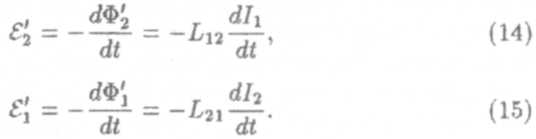
Примером применения явления взаимной индукции является та­кой прибор, как трансформатор.

Лекция № 31