Электромагнитные волны. Английский ученый Джеймс Клерк Максвелл в 1865 году, обобщив уравнения электромагнетизма, записал систему уравнений
Английский ученый Джеймс Клерк Максвелл в 1865 году, обобщив уравнения электромагнетизма, записал систему уравнений, которая позволяет решить практически любую электродинамическую задачу. В своей теории электромагнитного поля Максвелл использовал новое понятие — ток смещения, дал определение электромагнитного поля и предсказал существование в пространстве электромагнитных волн. Запишем систему уравнений Максвелла в дифференциальной форме:
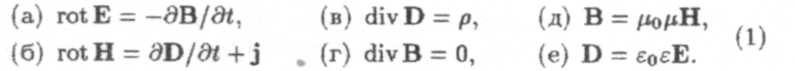
Здесь j — плотность тока, р — объемная плотность заряда, величина dD/dt называется плотностью тока смещения. Дифференциальные операторы rot и div определяются следующим образом. Вводится дифференциальный оператор набла (V)
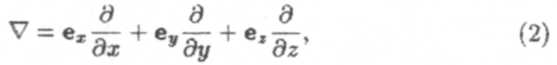
где ex, еу, ez,— единичные орты по осям x,y,z. Скалярное произведение
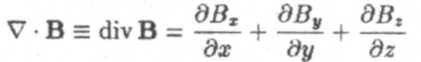
определяет операцию дивергенции. Векторное произведение V х Е = rot Е определяет операцию ротора.
С помощью системы (1) можно решить как прямую задачу, т.е. по известным источникам найти поля, так и обратную задачу, т.е. по известным полям определить источники.
Практическая задача о распространении электромагнитных (в частности, радиоволн) может быть достаточно сложной. Это связано с неоднородностью среды, анизотропией среды, сложностью рельефа поверхности, над которой происходит распространение, и другими особенностями задачи. Поэтому в качестве приложения системы (1) мы рассмотрим простую задачу о распространении плоской монохроматической волны в вакууме.
Плоская волна это такая волна, фронт которой представляет собой плоскость. Если волна распространяется вдоль оси х, то для полей в этом случае нет зависимости от координат у и г; д/ду = 0, д/dz = 0.
Монохроматической называется волна, поля которой меняются с течением времени по закону косинуса (coswt) или синуса (sinωt) при фиксированной частоте ω.
Рассмотрим в системе (1) поля вне источников j = 0,р = 0.Применяя операцию ротора к уравнению (1а) и воспользовавшись материальным соотношением (1д), получим
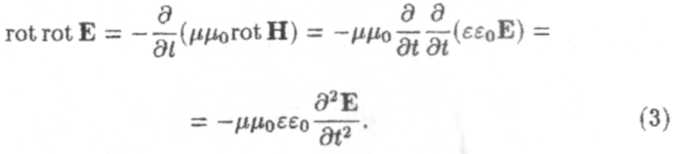
Палее воспользуемся рядом математических соотношений
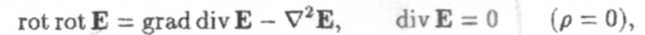
следовательно, rot rot Е = -  2E. Здесь
2E. Здесь  2 — оператор Лапласа, определяемый следующим образом:
2 — оператор Лапласа, определяемый следующим образом:
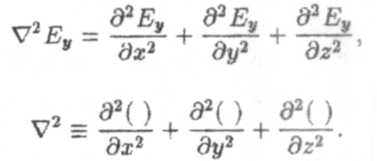
Значит, уравнение для поля Е принимает вид

Уравнение (4) описывает распространение электромагнитной волны в однородном пространстве. Лля выбранной зависимости от координат имеем
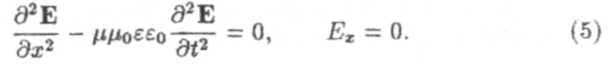
Для вакуума ε = μ= 1. Вводя обозначения е0 μ0= 1/с2 и направляя ось у вдоль Е, вместо (5) получим

Решением этого уравнения, как нетрудно убедиться (прямой подстановкой), является любая функция, зависящая от времени и координат следующим образом:
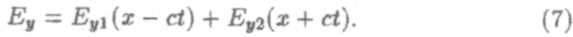
Функция Еу1 описывает волну, распространяющуюся в положительном направлении оси х, а функция Еу2 описывает волну, бегущую в отрицательном направлении оси х. В качестве частного случая рассмотрим плоскополяризованную монохроматическую волну, бегущую в положительном направлении оси х; тогда
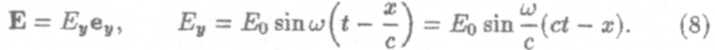
Эта волна бежит в положительном направлении оси х со скоростью с. Зафиксируем поверхность равной фазы ωt - (ω/c)x = const. Тогда с ростом t величина х также должна возрастать.
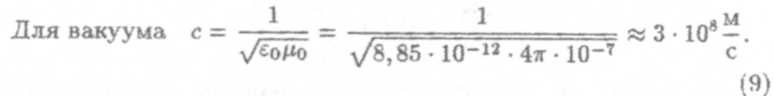
| Эта волна бежит в положительном направлении осих со скоростью с. Зафиксируем поверхность равной фазыω>t - (ω/c)x = const. Тогда с ростомt величинах также должнавозрастать. |
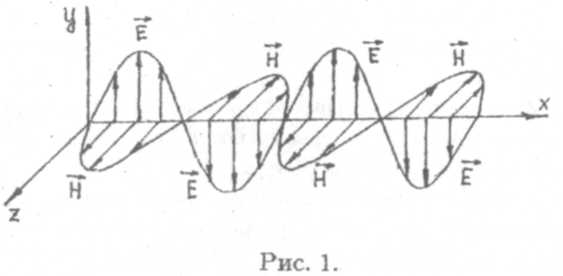
| скорость распространения электромагнитных волн в вакууме совпадает со скоростью света. Отсюда был сделан вывод, что свет представляет собой электромагнитную волну. Электромагнитные волны поперечны. В данном случае она имеет поляризацию (компоненты) (Ey,Hz) и схематически показана на рис. 1. |
Заметим, что плотность энергии для электрической и магнитной составляющей волны одинакова

Энергия и здесь равномерно распределяется по степеням свободы. Для излучения электромагнитных волн используется открытый колебательный контур. На высоких частотах в качестве колебательного контура используется просто отрезок провода, называемый вибратором. В зависимости от длины волны электромагнитные волны классифицируются следующим образом:

Теория Максвелла позволила создать современное радио и телевидение. Сфера приложения этой теории чрезвычайно разнообразна.
Лекция № 32
Дата добавления: 2015-08-11; просмотров: 944;
