Волновой пакет. Фазовая и групповая скорость электромагнитной волны
Всякая реальная электромагнитная волна представляет собой суперпозицию (наложение) волн, частоты которых заключены в некотором интервале Dw. Суперпозиция волн, мало отличающихся по частоте (или длине волн), называется волновым пакетом (или группой волн). Уравнение группы волн имеет вид:
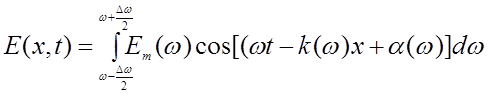. (2.5.1)
 |
Волны, образующие пакет, отличаются друг от друга по l, а, следовательно, и по
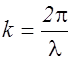. В некоторый момент времени t отличие по фазе складываемых волн для разных х будет различным, так как в одних точках волны усиливают друг друга больше, а в других меньше (рис.2.5.1).
В том месте, где в данный момент волны больше всего усиливают друг друга, будет наблюдаться максимум. С течением времени максимум будет перемещаться с некоторой скоростью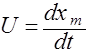 
- называемой групповой. Получим выражение для групповой скорости на примере наложения двух плоских волн с одинаковыми амплитудами и близкими частотами:
E1 =Emcos(wt-kx), (2.5.2)
E2 =Emcos[(w+Dw)t-(k+Dk)x)]. (2.5.3)
Будем считать, что Dw<<w; Dk<<k. Сложив уравнения (2.5.2) и (2.5.3) и произведя преобразования по формуле для суммы косинусов, получим уравнение результирующей волны:
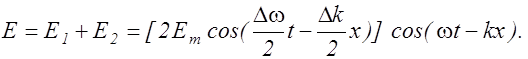(2.5.4)
Во втором множителе учтено, что Dw<<2w и Dk<<k.
Уравнение (2.5.4) можно рассматривать как уравнение плоской волны, амплитуда которой (выражение в квадратных скобках) медленно изменяется со временем. Максимум амплитуды в каждый фиксированный момент времени t соответствует координате xm, определяемой из условия
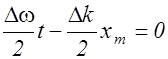. (2.5.5)
Согласно определению групповая скорость будет равна
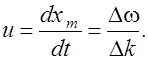
Переходя к дифференциалам, получим формулу
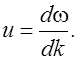(2.5.6)
Заменим в (2.5.6) w =Vk, где V - фазовая скорость, тогда получим
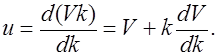(2.5.7)
Учтем, что по определению волновое число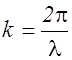 
, откуда 
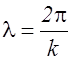. Заменим в (2.5.7) 
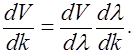Находим 
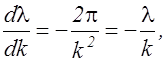поэтому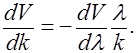 
Подставляя найденное для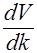 
выражение в формулу (2.5.7), получим
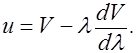(2.5.8)
Из формулы (2.5.8) следует, что в зависимости от знака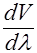 
групповая скорость u может быть как больше, так и меньше фазовой.
Если все составляющие группы волн распространяются в среде с одинаковой скоростью u(l)=const, то относительное расположение волн остается все время неизменным и центр пакета будет перемещаться со скоростью u=V.
Если фазовая скорость зависит от частоты (длины волны), то есть наблюдается дисперсия, то центр пакета перемещается со скоростью, определяемой формулой (2.5.8).
Дата добавления: 2015-07-22; просмотров: 3454;