Подставляя (2.4.3) в (2.4.2) и учитывая (2.4.4), получим
П=wV.(2.4.5)
Учтем, что энергия волны переносится в направление скорости ее распространения, тогда (2.4.5) можно записать в векторном виде.
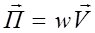 . (2.4.6)
. (2.4.6)
Выражение для вектора 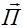 , впервые было получено русским ученым Н.А.Умовымдля упругих волн. Поэтому вектор
, впервые было получено русским ученым Н.А.Умовымдля упругих волн. Поэтому вектор 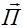 называется вектором Умова.
называется вектором Умова.
Найдем выражение для вектора плотности потока энергии, переносимой электромагнитной волной. Объемная плотность энергии в электромагнитной волне состоит из двух вкладов - от электрического и магнитного полей:
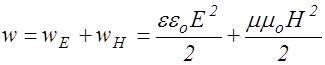 . (2.4.7)
. (2.4.7)
Векторы 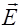 и
и  в электромагнитной волне изменяются в фазе (§ 2.3), поэтому выражение (2.4.7) справедливо не только для амплитудных значений [формула (2.3.43)], но и для мгновенных, причем
в электромагнитной волне изменяются в фазе (§ 2.3), поэтому выражение (2.4.7) справедливо не только для амплитудных значений [формула (2.3.43)], но и для мгновенных, причем
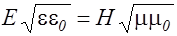 . (2.4.8)
. (2.4.8)
Из (2.4.8) и (2.4.7) следует, что объемная плотность энергии электрического и магнитных полей в электромагнитной волне в каждый момент времени одинакова, то есть 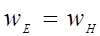 , поэтому справедливо:
, поэтому справедливо:
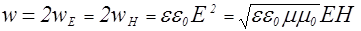 . (2.4.9)
. (2.4.9)
Электромагнитная волна распространяется в среде со скоростью
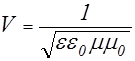 .
.
Подставим в формулу (2.4.5) выражения для w и V, тогда получим
П=Е Н. (2.4.10)
С учетом взаимной ориентации векторов 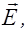
 и
и 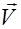 (рис.2.3.3), вектор плотности потока энергии можно записать в виде
(рис.2.3.3), вектор плотности потока энергии можно записать в виде
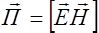 . (2.4.11)
. (2.4.11)
Выражение (2.4.11) было получено Пойнтингом, поэтому вектор 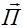 называется вектором Умова-Пойнтинга.
называется вектором Умова-Пойнтинга.
В электромагнитной волне векторы 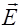 и
и  изменяются со временем с частотой n. Например, в видимом глазом диапазоне электромагнитных волн частота изменений векторов
изменяются со временем с частотой n. Например, в видимом глазом диапазоне электромагнитных волн частота изменений векторов 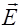 и
и  заключена в интервале
заключена в интервале
n = (0.75¸0.4)1015 Гц.
За столь частыми изменениями энергии не сможет уследить ни один приемник, вследствие чего будет регистрироваться усредненное по времени значение модуля вектора плотности потока энергии, которое называется интенсивностью волны:
J = < 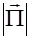 >.(2.4.12)
>.(2.4.12)
Получим выражения для интенсивности плоской и сферической электромагнитной волны.
Уравнения плоской и сферической электромагнитных волн, распространяющихся в произвольном направлении, имеют вид (2.2.14, 2.2.19, 2.2.20):
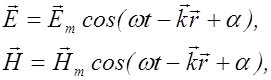 (2.4.13)
(2.4.13)
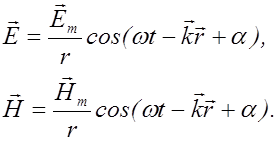 (2.4.14)
(2.4.14)
Подставляя модули векторов 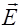 и
и  из (2.4.13) в формулу (2.4.10) и учитывая соотношение (2.3.44), находим плотность потока энергии переносимой плоской волной
из (2.4.13) в формулу (2.4.10) и учитывая соотношение (2.3.44), находим плотность потока энергии переносимой плоской волной
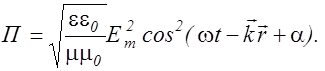 (2.4.15)
(2.4.15)
Подстановка 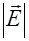 и
и 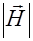 из (2.4.14) в (2.4.10) дает для плотности потока энергии в сферической волне выражение
из (2.4.14) в (2.4.10) дает для плотности потока энергии в сферической волне выражение
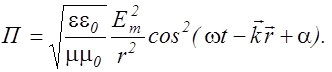 (2.4.16)
(2.4.16)
Для нахождения интенсивности волн (2.4.13) и (2.4.14) необходимо найти средние за период значения от выражений (2.4.15) и (2.4.16). Учтем, что

тогда для интенсивностей волн получим
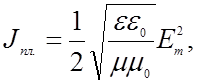 (2.4.17)
(2.4.17)
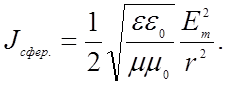 (2.4.18)
(2.4.18)
Зависимость амплитуды сферической волны от r в уравнениях (2.2.14), (2.4.14) связана с тем, что если среда не поглощает энергию волны, то средний поток энергии, проходящий через сферу любого радиуса, должен быть одинаков. Действительно, из (2.4.2) находим поток энергии через площадку D 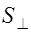 , расположенную перпендикулярно к направлению распространения волны:
, расположенную перпендикулярно к направлению распространения волны:
DФ=ПD 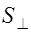 . (2.4.19)
. (2.4.19)
Для нахождения потока энергии через замкнутую поверхность S необходимо вычислить интеграл
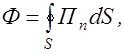 (2.4.20)
(2.4.20)
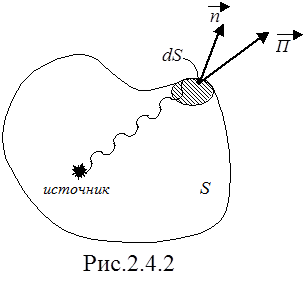
где Пn - нормальная составляющая вектора 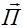 на произвольном элементе dS замкнутой поверхности (рис. 2.4.2).
на произвольном элементе dS замкнутой поверхности (рис. 2.4.2).
|
Усредненный по времени поток энергии переносимой сферической волной через сферу произвольного радиуса найдем согласно (2.4.20) по формуле
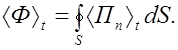 (2.4.21)
(2.4.21)
Направления распространения сферической волны и нормали к любому элементу сферической поверхности совпадают, поэтому
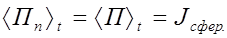
Воспользовавшись выражением (2.4.17) для Jсфер из (2.4.21) получим
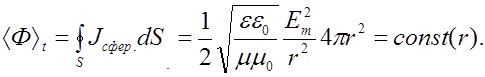

Дата добавления: 2015-07-22; просмотров: 1526;
