Волновой процесс. Уравнение плоской волны. Волновое уравнение.
Волной называется процесс распространения колебания (или какого-то другого сигнала) в пространстве.
Представим, например, что во всех точках плоскости YOZ некоторый физический параметр меняется во времени по гармоническому закону
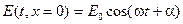 .
.
Пусть колебания этого абстрактного параметра распространяются вдоль оси OX со скоростью v (рис. 13.1.). Тогда в плоскости с координатой x исходные колебания повторятся вновь, но с запаздыванием на 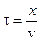 секунд:
секунд:
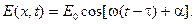 (13.1)
(13.1)
Рис. 13.1.
Функция (13.1) называется уравнением плоской волны. Эту важную функцию чаще записывают в таком виде
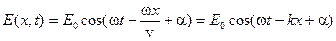 . (13.2)
. (13.2)
Здесь: Е0 и w — амплитуда и частота колебаний в волне,
(wt – kx +  — фаза волны,
— фаза волны,
a — начальная фаза,
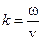 — волновое число,
— волновое число,
v — скорость распространения волны.
Совокупность всех точек пространства, в которых колебания происходят в одинаковой фазе, определяет фазовую поверхность. В нашем примере это плоскость.
(wt – kx +  = F = const — уравнение движения фазовой поверхности в процессе распространения волны. Возьмём производную этого уравнения по времени:
= F = const — уравнение движения фазовой поверхности в процессе распространения волны. Возьмём производную этого уравнения по времени:
w – k 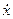 = 0.
= 0.
Здесь 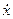 = vф — скорость движения фазовой поверхности — фазовая скорость.
= vф — скорость движения фазовой поверхности — фазовая скорость.
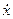 = vф =
= vф = 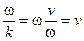 .
.
Таким образом, фазовая скорость равна скорости распространения волны.
Фазовая поверхность, отделяющая пространство, охваченное волновым процессом, от той части, куда волна еще не дошла, называется фронтом волны. Фронт волны, как одна из фазовых поверхностей, тоже движется с фазовой скоростью. Эта скорость, например, акустической волны в воздухе составляет 330 м/с, а световой (электромагнитной) волны в вакууме — 3×108 м/с.
Уравнение волны Е = Е0×cos(wt – kx + j) представляет собой решение дифференциального волнового уравнения. Для отыскания этого дифференциального уравнения, продифференцируем уравнение волны (13.2) дважды по времени, а затем — дважды по координате:
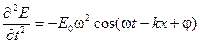 ,
,
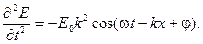
Сравнив эти два выражения, обнаруживаем, что
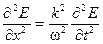 .
.
Но волновое число k = 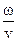 , поэтому
, поэтому
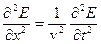 . (13.3)
. (13.3)
Это и есть дифференциальное уравнение волнового процесса — волновое уравнение.
Еще раз отметим, что уравнение волны (13.2) есть решение волнового уравнения (13.3).
Волновое уравнение можно записать, конечно, и так
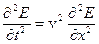 .
.
Теперь очевидно, что в волновом уравнении коэффициент при второй производной по координате равен квадрату фазовой скорости волны.
-*-
Если, решая задачу о движении, мы получаем дифференциальное уравнение типа
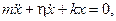
то это означает, что исследуемое движение — собственные затухающие колебания…
Если при решении очередной задачи возникло дифференциальное уравнение
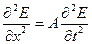 ,
,
то это означает, что исследуется волновой процесс, и скорость распространения этой волны 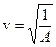 .
.
Дата добавления: 2015-08-08; просмотров: 1449;
