Энергия магнитного поля

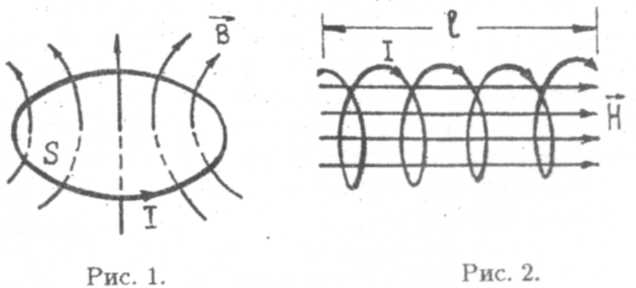
Рассмотрим контур, по которому течет ток силой I (рис. 1). Этот ток в пространстве вокруг себя порождает магнитное поле, силовые линии которого пронизывают площадь, ограниченную контуром с током, создавая через нее магнитный поток Ф.

Тогда коэффициент пропорциональности между током в кон­туре I и магнитным потоком Ф, который данный ток создает

через контур, называется индуктивностью контура L. В системе СИ индуктивность измеряется в генри (Гн).

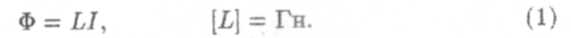
Индуктивность контура зависит от его размеров, формы и маг­нитной проницаемости ц окружающей среды.

Подсчитаем теперь энергию магнитного поля, связанного с контуром тока. Для этого будем полагать, что в начальный мо­мент ток в контуре отсутствует. Вычислим, какую надо совер­шить работу по замагничиванию контура; тогда

Здесь мы полагаем, что L = const. Интегрируя (2), имеем

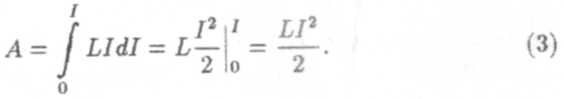
Вследствие закона сохранения энергии работа по замагничива­нию контура будет равна энергии магнитного поля, связанного с контуром. Отсюда

В качестве примера расчета индуктивности проводника найдем индуктивность соленоида — катушки с током. Будем считать, что длина соленоида I > D — диаметра его поперечного сечения и витки соленоида плотно прилегают друг к другу (рис. 2). Пло­щадь поперечного сечения соленоида S, общее число витков N. Тогда внутри соленоида магнитное поле будет однородным, его напряженность определяется по формуле Н = nl. Здесь п = N/l — число витков на единицу длины. Отсюда В=μ₀ μH=μ₀ μnI, а Ф₁ =μ₀ μnIS — поток магнитной индукции через один виток соле­ноида. Тогда поток вектора В через все N = nl витков соленоида Ф определится по формуле

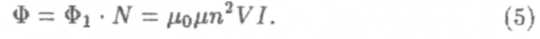
Здесь V =S ∙ I — объем соленоида. Следовательно, индуктив­ность соленоида будет равна

Здесь μ — магнитная проницаемость среды, заполняющей соле­ноид. Воспользовавшись (6), найдем энергию магнитного поля катушки с током

Теперь рассчитаем плотность энергии магнитного поля W, т.е. его энергию, содержащуюся в единице объема.

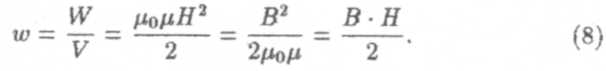
Здесь мы учли, что Н = nl и В =μ₀ μH. Любая из формул (8) может быть использована для подсчета плотности энергии маг­нитного поля. Какую именно из этих формул надо использовать, зависит от конкретной задачи. Как показано в более строгой теории, формулы (8) справедливы при любой конфигурации маг­нитного поля, а не только для поля соленоида.