Проводникас током в магнитном поле

Для наглядности рассмотрим случай, когда скорость про­водника направлена перпендикулярно к силовым линиям магнит­ного поля и к проводнику. Однако прежде введем понятие потока вектора магнитной индукции.

Пусть у нас есть плоский контур площадью S, который про­низывают силовые линии индукции В однородного магнитного поля (рис. 2).

Потоком вектора магнитной индукции В через данный кон­тур называется скалярная величина Ф, равная произведению мо­дуля индукции В на площадь контура 5 и на cos а. Здесь угол а берется между вектором единичной нормали п к поверхности S и силовой линией магнитной индукции

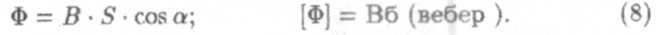
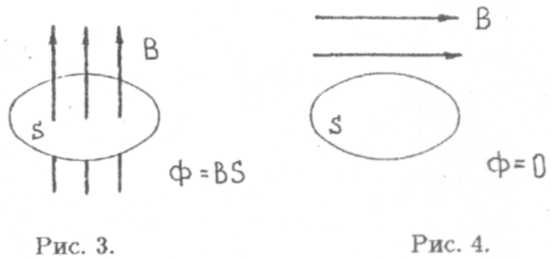
Очевидно, что поток вектора индукции максимален, когда сило­вые линии перпендикулярны контуру (рис. 3) и равен нулю, когда силовые линии В параллельны поверхности S (рис. 4).

Рассмотрим теперь работу по перемещению проводника с то­ком в магнитном поле. На рис. 5 магнитное поле показано точка­ми в кружках. Это означает, что вектор магнитной индукции на­правлен перпендикулярно плоскости рисунка к нам. Длина про­водника l, I — сила тока в проводнике, x — расстояние, на кото­рое сила Ампера перемещает проводник. Как известно, работа силы определяется по формуле А — F» • х. В данном случае на­правления силы и перемещения совпадают. Подставляя значение силы Ампера, найдем

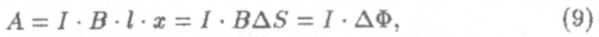
где ∆S = l∙х — площадь, пересекаемая проводником за рассма­триваемый промежуток времени, ∆Ф — поток вектора магнитной индукции через пересекаемую проводником площадь.

Тогда формулу для работы по перемещению проводника с током в магнитном поле можно представить в форме А = I∆Ф или в дифференциальном виде

Формулы (9) и (10) оказываются универсальными, подходящими для любых случаев движения проводника в магнитном поле. В дальнейшем мы используем эти формулы для расчета энергии магнитного поля проводника с током.

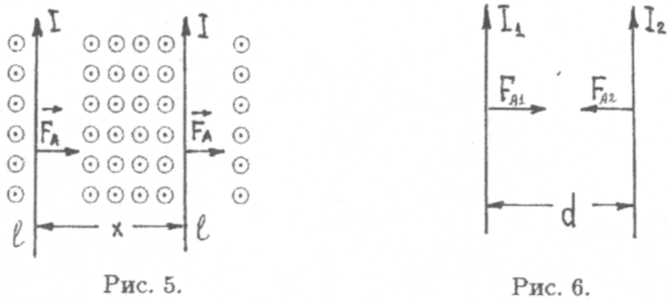
В заключение приведем пример использования закона Ампера для расчета взаимодействия токов. По двум бесконечным прямолинейным проводникам в одном направлении текут токи I₁и I₂(рис. 6). Расстояние между проводниками d. Тогда, исполь­зуя формулу для напряженности магнитного поля бесконечного прямолинейного провода и закон Ампера, нетрудно показать, что сила взаимодействия между проводниками, приходящаяся на ка­ждый метр длины, будет равна

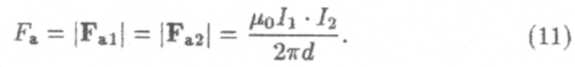
Здесь μ₀— магнитная постоянная (мы предполагаем, что провод­ники находятся в вакууме); если токи текут в одном направлении, то проводники притягиваются друг к другу. На основе формулы (11) вводится одна из основных единиц системы СИ — ампер (А).

Ампером называется такая сила неизменяющегося тока, те­кущего по каждому из двух прямолинейных параллельных беско­нечно длинных проводов, находящихся в вакууме на расстоянии 1 метр друг от друга, при которой проводники взаимодействуют между собой с силой 2 ∙ 10 ^-7 Н на каждый метр длины.

Лекция № 29