Генерация шума турбулентным потоком
Основные источники шума в авиации имеют аэродинамическое происхождение. При этом акустическое излучение генерируется либо свободными турбулентными потоками (реактивная струя газов ГТД), либо при взаимодействии турбулентного потока с жесткими границами (шум лопаточных машин ГТД, шум обтекания планера, шум турбулентного пограничного слоя).
Впервые теоретические вопросы образования звука при движении жидкости были рассмотрены в 1877г в классической работе Рэлея «Теория звука». Попытка решения задачи о распространении звука в движущейся среде для случая безвихревого движения среды с малыми возмущениями была предпринята в 1934г Н.Н. Андреевым и И.Г. Русаковым. Первое решение задачи об источниках аэродинамического шума было получено в 1935-36 г Л.Я. Гутиным, который получил аналитическое выражение для уровня звукового давления в дальнем акустическом поле воздушного винта. В 1942 г. Е.Я. Юдин, используя методы теории подобия, установила для шума вихревого происхождения зависимость интенсивности шума от скорости обтекания твердого тела в «шестой степени». Важным шагом в изучении аэродинамических шумов явилось создание в 40-х годах прошедшего столетия Д.И. Блохинцевым теории распространения звука в движущейся среде.
В начале 50-х годов появились работа М. Лайтхилла, в которой впервые была выдвинута и использована идея акустической аналогии для решения задачи о генерации шума свободным турбулентным потоком. В конце 50-х годов Н. Керл распространил акустическую аналогию М. Лайтхилла на случай генерации звука турбулентным потоком в присутствии жестких границ. В последующем предпринимались неоднократные попытки расширить математический аппарат акустической аналогии, однако это не привело к улучшению исходной модели М. Лайтхилла в части понимания и решения проблемы шума турбулентной струи. Теория М. Лайтхилла основана на преобразовании уравнений непрерывности и сохранения импульса (уравнений Навье-Стокса) для сжимаемой жидкости при малых числах Маха в неоднородное волновое уравнение.
В рамках настоящего курса мы рассматриваем только основные положения акустической аналогии М. Лайтхилла и вывод неоднородного волнового уравнения Лайтхилла - Керла.
Уравнение Лайтхилла – Керла может быть получено на основе комбинации уравнений неразрывности и количества движения.
Уравнение неразрывности в тензорной форме имеет следующий вид:
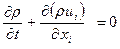 , (5.1)
, (5.1)
где t – время, ρ – плотность, ui – cскорость течения потока в направлении хi, Уравнение количества движения в тензорной форме имеет следующий вид:
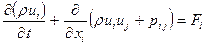 , (5.2)
, (5.2)
где Fi – сила, действующая на единицу объема среды, ρuiuj – тензор касательных напряжений Рейнольдса, а тензор
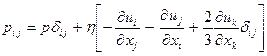
- тензор напряжений от сил давления и вязкости; η – коэффициент сдвиговой вязкости;
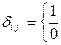 - символ Кронекера, равный 1 – при i=j, и равный 0 – при i ≠ j.
- символ Кронекера, равный 1 – при i=j, и равный 0 – при i ≠ j.
Если продифференцировать уравнение неразрывности по времени, а уравнение количества движения – по пространству (по координате хi ) и вычесть одно из другого, то получим:
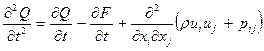 .
.
Прибавив и вычтя из правой части последнего соотношения выражение 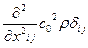 , получим неоднородное волновое уравнение в форме Лайтхилла – Керла:
, получим неоднородное волновое уравнение в форме Лайтхилла – Керла:
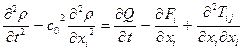 , (5.3)
, (5.3)
где 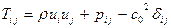 - тензор напряжений, представляющий собой разность между напряжениями в потоке и напряжениями в однородной покоящейся среде. Учитывая сложность решения уравнения (5.3) М. Лайтхилл предложил рассматривать правую часть как эквивалентное нестационарному потоку распределение акустических источников, которые излучают звуковые волны в идеальную среду, находящуюся в состоянии покоя (акустическая аналогия).
- тензор напряжений, представляющий собой разность между напряжениями в потоке и напряжениями в однородной покоящейся среде. Учитывая сложность решения уравнения (5.3) М. Лайтхилл предложил рассматривать правую часть как эквивалентное нестационарному потоку распределение акустических источников, которые излучают звуковые волны в идеальную среду, находящуюся в состоянии покоя (акустическая аналогия).
Итак, правая часть неоднородного волнового уравнения представляет аэродинамические источники акустического излучения, а левая часть уравнения описывает распространение звуковых волн. Если в потоке имеются источники с производительностью “Q”, то в процессе изменения их производительности генерируется акустическое излучение; если имеются массовые силы, то изменение их в пространстве также является источником звуковых волн. Последний член в правой части уравнения отражает влияние тензора напряжений на генерацию звука потоком.
Общее решение уравнения (5.3) включает в себя три члена, описывающие, соответственно, источники монопольного, дипольного и квадрупольного типов, и состоит из интегралов по объему жидкости и по поверхности, обтекаемой жидкостью:
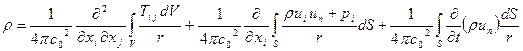 (5.4)
(5.4)
 здесь рi – величина аэродинамической нагрузки, действующей со стороны потока на поверхность S в направлении xi, un – нормальная к поверхности составляющая скорости потока вблизи поверхности.
здесь рi – величина аэродинамической нагрузки, действующей со стороны потока на поверхность S в направлении xi, un – нормальная к поверхности составляющая скорости потока вблизи поверхности.
Отдельные составляющие решения (5.4) интерпретируются следующим образом. Объемный интеграл соответствует источникам типа квадруполь, распределенным по объему поля течения вдали от жесткой границы.
Второй интеграл описывает излучение источниками типа диполь, распределенными на обтекаемой поверхности S. Эти источники определяются пульсациями давления и вязкими напряжениями. Параметр 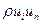 характеризует скорость изменения импульса, которая равна нулю в случае жесткой или колеблющейся в собственной плоскости границы, а для случая перемещающейся границы этот параметр характеризует обмен количеством движения между близлежащими слоями жидкости. Параметр рi характеризует силу воздействия потока на жесткую границу.
характеризует скорость изменения импульса, которая равна нулю в случае жесткой или колеблющейся в собственной плоскости границы, а для случая перемещающейся границы этот параметр характеризует обмен количеством движения между близлежащими слоями жидкости. Параметр рi характеризует силу воздействия потока на жесткую границу.
Третий интеграл описывает акустическое излучение источниками монопольного типа, которые расположены на поверхности S и отражают собой вытеснение среды из области пространства, обусловленное движением поверхности S. Для жестких неподвижных поверхностей нормальная составляющая скорости на поверхности un=0, и в этом случае монопольные источники отсутствуют. В случае мягкой (податливой) поверхности третий интеграл в решении (5.4) не равен нулю и в общем акустическом излучении потока будет присутствовать составляющая, обусловленная пульсациями вблизи поверхности нормальной к поверхности составляющей скорости потока.
При отсутствии жестких границ второй и третий интегралы в решении (5.4) отсутствуют и оно переходит в известное решение Лайтхилла, учитывающее только источники квадрупольного типа.
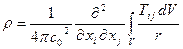 (5.5)
(5.5)
Если мгновенную скорость разложить на осредненную 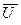 и пульсационную
и пульсационную 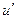 составляющие, , то есть
составляющие, , то есть 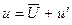 , то сохраняя в правой части уравнения Лайтхилла (5.5) только члены, отвечающие за генерирование шума турбулентным потоком, получим соотношение (5.6), позволяющее объяснить некоторые механизмы генерации шума турбулентным потоком.
, то сохраняя в правой части уравнения Лайтхилла (5.5) только члены, отвечающие за генерирование шума турбулентным потоком, получим соотношение (5.6), позволяющее объяснить некоторые механизмы генерации шума турбулентным потоком.
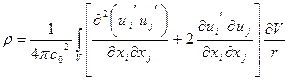 (5.6)
(5.6)
Первое слагаемое подинтегрального выражения содержит пространственные производные пульсационных скоростей и отвечает за взаимодействия типа «турбулентность – турбулентность». Второе слагаемое представляет собой произведение градиента средней скорости и пространственной производной пульсационной составляющей скорости и соответствует взаимодействию типа «сдвиг средней скорости – турбулентность».
В соответствии с существующей терминологией первое слагаемое определяет «собственный» шум турбулентности, а второе – «сдвиговый» шум.
В уравнении (5.5) функция источников шума Tij определяется вторыми производными по координатами от элементов тензора полных напряжений. Тензор Tij представляет собой разность между эффективными напряжениями в потоке и напряжениями в однородной покоящейся среде. В соответствии с акустической аналогией флуктуации плотности в турбулентной движущейся среде будут совпадать с флуктуациями плотности в невозмущенной среде, если среда находится под воздействием внешних сил Tij.
Таким образом, точные уравнения движения жидкости могут быть записаны как как уравнения распространения звука в покоящейся среде, а действие потока можно заменить полем внешних напряжений (сил), которое воздействует на среду, вызывая в ней флуктуации плотности.
Уравнение (5.5) для фиксированной системы координат записывается в следующем виде:
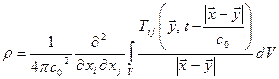 (5.7)
(5.7)
где 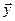 - координаты элемента объема жидкости dV,
- координаты элемента объема жидкости dV, 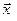 - координаты точки наблюдения, расположенной вне поля потока в дальнем акустическом поле,
- координаты точки наблюдения, расположенной вне поля потока в дальнем акустическом поле, 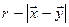 - расстояние от источника (элемента объема жидкости) до точки наблюдения. Отметим, что изменение плотности в точке поля, расположенной на удалении “r” от источника, определяется тензором напряжений “Tij” с некоторой задержкой времени
- расстояние от источника (элемента объема жидкости) до точки наблюдения. Отметим, что изменение плотности в точке поля, расположенной на удалении “r” от источника, определяется тензором напряжений “Tij” с некоторой задержкой времени 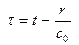 . Запаздывание обусловлено временем прохождения звуковой волны расстояния “r”. Звуковое давление вне потока определяется соотношением
. Запаздывание обусловлено временем прохождения звуковой волны расстояния “r”. Звуковое давление вне потока определяется соотношением 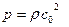 .
.
Выполнив дифференцирование в правой части уравнения (5.7), и имея ввиду, что
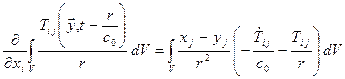 ;
;
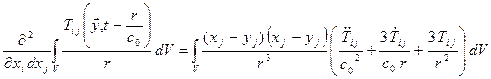 ;
;
получим:
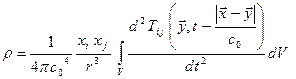 . (5.8)
. (5.8)
Известно, что пульсации скорости хорошо коррелированны в близко расположенных точках пространства, и слабо коррелированны в удаленных друг от друга точках. Поэтому все поле течения жидкости можно представить состоящим из элементарных объемов, внутри которых пульсации скорости коррелированны. Флуктуации плотности, создаваемые коррелированными источниками, суммируются амплитудно, а некоррелированными источниками – суммируются энергетически, то есть складываются среднеквадратичные значения давления или интенсивности.
Допустимая величина элементарного объема жидкости определяется порядком максимально возможных изменений задержки времени в уравнении (5.8). Если в качестве характерного размера источника взять средний масштаб корреляции “  ”, то задержкой времени в пределах элементарного объема можно пренебречь. В самом деле масштаб корреляции можно рассматривать как размер типичного акустического источника, и для акустически эффективного источника он должен быть мал по сравнению с длиной волны излучаемого звука, то есть
”, то задержкой времени в пределах элементарного объема можно пренебречь. В самом деле масштаб корреляции можно рассматривать как размер типичного акустического источника, и для акустически эффективного источника он должен быть мал по сравнению с длиной волны излучаемого звука, то есть
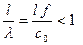 .
.
Это условие выполняется при относительно низких скоростях движения среды, поскольку произведение ( 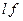 ) равно характерной скорости потока. Однако если рассматривать частоту “f” в связанной с источником системе координат, то произведение (
) равно характерной скорости потока. Однако если рассматривать частоту “f” в связанной с источником системе координат, то произведение ( 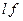 ) можно трактовать как пульсационную составляющую скорости потока, которая не превышает величины 10%-15% от средней скорости течения, и последнее условие выполняется для всех дозвуковых течений.
) можно трактовать как пульсационную составляющую скорости потока, которая не превышает величины 10%-15% от средней скорости течения, и последнее условие выполняется для всех дозвуковых течений.
Если пренебречь изменением времени запаздывания внутри элементарного объема с характерным размером “  ”, то значение подинтегрального выражения в соотношении (5.8) можно принять равным его значению в центре элементарного объема. Тогда соотношение (5.8) можно записать в виде:
”, то значение подинтегрального выражения в соотношении (5.8) можно принять равным его значению в центре элементарного объема. Тогда соотношение (5.8) можно записать в виде:
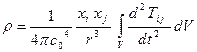 . (5.9)
. (5.9)
Поскольку для дальнего акустического поля 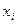 ~ r, а в пределах самого потока
~ r, а в пределах самого потока
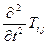 ~
~ 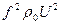 ,
,
где U – средняя скорость течения, f – характерная частота пульсаций скорости в потоке (f ~ U/  ), то :
), то :
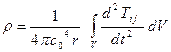 ~
~ 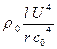 . (5.10)
. (5.10)
Пульсация плотности в среде вне потока, то есть в звуковой волне, пропорциональна скорости течения в четвертой степени.
Выражение для мощности акустического излучения имеет следующий вид:
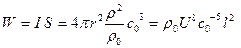 (5.11)
(5.11)
Дата добавления: 2015-07-18; просмотров: 4358;
