Генерация мультимножеств.

Для представления данных некоторых задач более естественными, чем множества являются множества с повторениями элементов, или мультимножества. При записи мультимножеств с каждым элементом удобно связывать неотрицательное целое число, указывающее количество повторений этого элемента.

Пример. Мультимножество (x, x, x, y, y, z, z, z, u) удобно записывать как (3×x, 2×y, 3×z, 1×u).

Применение коэффициентов кратности удобно также для представления мультимножеств при построении алгоритмов. Пусть x<y<z<u, тогда множество (3×x, 2×y, 3×z, 1×u) представимо как (3,2,3,1).

Таким образом, если для представления подмножеств некоторого базового множества из n элементов были использованы n-последовательности нулей и единиц, то для представления мультимножеств, которые можно построить на базе этого множества, удобно использовать n-кортежи неотрицательных целых чисел.

Упражнения. 1. Пусть задано мультимножество A=(m₁,....,m_n), m_i³0, 1£i£n. Доказать, что А имеет 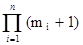мультиподмножеств.

2. Пусть A=(m,...,m), где базовое множество содержит n элементов. Написать программу генерации всех мультиподмножеств А в лексикографическом порядке. заметим, что подобная генерация фактически совпадает с выводом всех чисел от 0 до mⁿ-1 d m-ричной позиционной системе.

3.Написать программу генерации всех мультиподмножеств А из предыдущего упражнения, при котором каждое последующее мультиподмножество отличается от предыдущего вставкой или удалением одного элемента. Генерация начинается с представления пустого множества. (Вначале постройте рекурсивный алгоритм генерации, например, воспользовавшись последовательностью

C₁0; C₂0; ...; C_P0; C_P1; ...; C₁1; C₁2;...; C_P2; C_P3;. . . ,где р=mⁿ,

которая определяет генерацию мультимножеств (n+1)-го порядка. Затем постройте итеративный алгоритм, подобный SET3.)