File of T

где T – определение типа компонент файла.

С помощью этого определения можно описывать переменные, значения которых будут файлы.

С особенностью размещения файлов связано еще одно ограничение, накладываемое на работу с переменной типа файла: нельзя присваивать такой переменной новое значение с помощью оператора присваивания и передавать значение такой переменной в процедуру или функцию. Это ограничение не относится к передаче параметров- переменных в процедуру.

Изменение значений переменных типа файла происходит путем добавления или удаления компонент файла с помощью стандартных процедур обработки файлов.

Файлы могут быть внешними и внутренними (локальными). Локальные файлы создаются при входе в ту подпрограмм, где они описаны, и уничтожаются при выходе из нее. Такие файлы могут физически располагаться как во внешней, так и в оперативной памяти.

Пример. Заголовок программы с описанием файлов.

Program p (output, f1, f2);

type элемент=record

ключ: integer;

строка: string

end;

var f,f1,f2: file of элемент;

f1,f2 – внешние файлы, f – локальный

output – стандартный для ввода.

Замечание. Поскольку работа любой программы состоит в конечном итоге в том, что изменяется содержимое файлов, являющихся параметрами программы, то свойство любой программы можно выразить, описав, какие преобразования над файлами она выполняет.

Например. НОД(a,b)

Вначале input=<a,b>,b¹0

После output=<g>, где g=НОД(a,b).

В Турбо Паскале существуют три класса файлов: типизированные, текстовые и нетипизированные. Для типизированных указан тип компонент файла; в текстовых компоненты имеют стандартный тип TEXT; в нетипизированных компоненты представляют собой конечные совокупности символов или байтов, при этом представление char или byte не играют никакой роли|, а важно лишь с точки зрения объема занимаемых данных.

Файловая система Турбо Паскаля ориентирована на возможности операционной системы DOS. Каждому файлу в языке ставится в соответствие файловая переменная определенного типа. Поэтому перед началом работы с файлом необходимо установить соответствие. Для этого в языке используется процедура:

assign(f, name: string),

где f – переменная любого файлового типа, а строковое выражение name содержит полное имя файла удовлетворяющее требованием операционной системы.

Пример. assign(f1,’c:\kostin\tree.text)

Чтобы начать работу с файла необходимо его открыть. Работа с неоткрытым файлом считается ошибкой. Открытие осуществляется двумя способами в зависимости от характера будущей работы с файлом. Если файл открывается для чтения, его содержимое изменяться не может. Если файл открывается для записи, то это означает, что файл будет создаваться заново, при этом содержащаяся в нем информация ранее уничтожается, а новые компоненты присоединяются к концу файла, начиная с первой.

Открытие файла осуществляется стандартными процедурами:

reset(f) – для чтения; rewrite(f) – для записи.

В дальнейшем в любой момент времени файл можно “переоткрывать”, т. е. файл, первоначально открытый для чтения, может быть в последствие открыт для записи, и наоборот.

Организация ввода-вывода.

Стандартные процедуры и функции для всех файлов.

Процедуры:

Assign (F, Name) – связь файловой переменной с внешним файлом, имеющим имя Name. Name – переменная или константа типа string (или совместимого для присваивания с ним типа) или типа PСhar. Имя типа должно быть написано в соответствии с правилами MS DOS, может включать путь и не должно превышать 79 символов. Если строка имени пустая, осуществляется связь со стандартными файлами ввода или вывода.

Reset(F[,Size]) – открытие существующего файла.

Открывается существующий файл, с которым связана файловая переменная F, и указатель текущей компоненты файла настраивается на начало файла. Необязательный параметр целого типа Size используется только с файлами без типа и задает размер пересылаемого элемента информации в байтах. По умолчанию этот размер равен 128.

Rewrite(F[,Size]) –открытие нового файла.

Открывается новый пустой файл, и ему присваивается имя, заданное процедурой Assign. Если файл с таким именем уже существует, то он уничтожается. Необязательный параметр Size имеет тот же смысл, что и в процедуре Reset.

Close(F) –закрытие внешнего файла.

Закрывает внешний файл, с которым связана файловая переменная F. При этом в случае необходимости в содержимое файла вносятся все произведенные изменения.

Функции:

Eof(F)– конец файла.

Принимает значение true, если указатель текущей компоненты находится за последней компонентой файла (за последним символом, если файл текстовой), и false – в противном случае.

IOResult –результат последней операции ввода-вывода.

Возвращает значение 0, если операция ввода- вывода завершилось успешно, и другое число – в противном случае. После применения этой функции параметр состояния последней операции ввода-вывода сбрасывается в 0.

Стандартные процедуры и функции для текстовых файлов.

Текстовой файл представляет собой совокупность символов, разделенных на строки, причем в конце каждой строки стоит признак конца строки.

Особенностью работы с текстовыми файлами является то, что значения которые вводятся и выводятся с помощью процедур read или write, могут быть не обязательно типа Char или String, а также и других стандартных простых типов. Эти процедуры могут также работать и с ASCIIZ-строками.

Имеется две стандартные файловые переменные для текстового файла: input (для ввода с клавиатуры) и output (для вывода на экран дисплея).

Файл типа Text может быть открыт либо для чтения процедурой reset, либо для записи процедурой rewrite или append.

Процедуры:

Append(f) –открытие файла для добавления в конец информации.

Открывается существующий файл, с которым связанафайловая переменная F, и указатель текущей компоненты файла настраивается на конец файла.

Read(F,<список ввода) – чтение информации из файла.

Из файла, с которым связана файловая переменная F, читаются значения для одной или нескольких переменных списка ввода.

ReadLn(F,<список ввода) – чтение информации из файла.

То же, что и процедура read, но непрочитанная часть строки, включая признак конца строки, пропускается.

Write(F,<список вывода>) –запись информации в файл.

В файл, с которым связана файловая переменная F, записываются значение выражений списка вывода.

WriteLn(F,<список вывода>) –запись информации в файл.

То же, что и процедура write, но выводимая информация завешается признаком конца строки.

Функции:

Eoln(F)– конец строки файла.

Принимает значение true, если текущей компонентой файла является признак конца строки или функция eof(F) принимает значение true. В остальных случаях функция принимает значение false.

Стандартные процедуры и функции для типизированных файлов.

Процедуры:

Read(F,<список ввода) – чтение информации из файла.

То же, что и процедура read для текстовых файлов, но переменные, в которые читается информация, должны быть того же типа, что и компонента файла.

Write(F,<список вывода>) –запись информации в файл.

То же, что и процедура write для текстовых файлов, но список вывода представляет собой переменные того же типа, что и компонента файла.

Seek(F,Num)– настройка на требуемую компоненту файла.

Осуществляется настройка на компоненту файла, с которым связана файловая переменная F. Компонента файла определяется номером Num, причем нумерация начинается с нуля.

Truncate(F) –удаление части файла, начиная с текущей позиции.

Удаляется часть файла, начиная с текущей позиции и до его конца.

Функции:

FilePos(F)– номер текущей компоненты файла.

Функция возвращает номер текущей компоненты файла, с которым связана файловая переменная F. Нумерация начинается с нуля.

FileSize(F)– текущий размер файла.

Функция возвращает текущий размер файла, с которым связана файловая переменная F,в компонентах этого файла.

Задача. Задан файл, каждая компонента которого состоит из целого числа (ключа) и 80 – символов текста (данных). Требуется переписать содержимое этого файла в другой файл, изменив содержимое одной его компоненты с заданным ключом. Ключ и новое содержимое компоненты задаются в качестве исходных данных во входном потоке. Если компоненты с заданным ключом нет в исходном файле, то новая компонента добавляется в конец файла. Если в исходном файле есть несколько компонент с заданным ключом, то обновляется первая из таких компонент.

Решение:

Считаем input – содержит исходный данные;

output – для вывода сообщений о ходе работы программы;

а – исходный файл;

b – формируемый файл.

Работа программы будет состоять из двух фаз. На первой фазе содержимое файла а переписывается в файл b, пока не встретится компонента с заданным ключом. На второй фазе остаток файла а дописывается в файл b. Процесс заканчивается, когда будет исчерпано содержимое файла а.

Логическая переменная naid в программе имеет значение true только после того как ключ с заданным значением обнаружен.

program ff1 ;

type rec=record

kl:integer;

ct:string[80]

end;

var r,nov:rec;

a,b:file of rec;

i: integer;

naid: boolean;

begin

with nov do

begin

readln(kl);

readln(ct)

end;

assign(a,'c:\pas\pasv\f1.txt');

assign(b,'c:\pas\pasv\f2.txt');

reset(a);

rewrite(b);

naid:=false;

while not(naid or eof(a)) do

begin read(a,r);

if nov.kl=r.kl then naid:=true else write(b,r)

end;

write(b,nov);

while not eof(a) do

begin

read(a,r);

write(b,r)

end;

writeln(‘перепись завершена’);

close(a);

close(b)

end.

Файл а можно создать следующей программой:

program ff2 ;

type rec=record

kl:integer;

ct:string[80]

end;

var r:rec;

a:file of rec;

i: integer;

begin assign(a,'c:\pas\pasv\f1.txt');

rewrite(a);

for i:=1 to 5 do

with r do

begin

readln(kl);

readln(ct);

write(a,r)

end;

close(a)

end.

Упражнение. Рассмотреть задачу упорядочивания по ключам компонент файла (метод слияния).

Линейные списки.

program ref(input,output);

type YK=^EL;

EL=record

VAL:integer;

REF:YK

end;

var X:YK;

procedure SN1(var Z:YK);

var A:integer;

Y:YK;

begin Z:=nil;

read(A);

while A<>0 do

begin new(Y);

Y^.VAL:=A; Y^.REF:=Z;

Z:=Y; read (A);

end

end;

procedure S1N(var Z:YK);

var A: integer;

Y:YK;

begin Z:=nil;

read (A);

if A<>0 then

begin

new(Y);

Z:=Y;

Y^.VAL:=A;

read (A);

while A<>0 do

begin new(Y^.REF);

Y:=Y^.REF;

Y^.VAL:=A;

read (A);

end;

Y^.REF:=nil;

end

end {S1N};

procedure PS(X:YK);

begin writeln;

while X<>nil do

begin write(X^.VAL,' ');

X:=X^.REF

end;

writeln

end;

procedure S1NR(var X:YK);

var A:integer;

begin read (A);

if A<>0 then

begin new(X);

X^.VAL:=A;

S1NR(X^.REF)

end

else

X:=nil

end;

procedure YS(var X:YK);

var A: integer;

Z,Y,U :YK;

T:boolean;

begin read(A);

if A<>0 then

begin new (X);

X^.REF:=nil;

X^.VAL:=A;

read (A)

end;

while A<>0 DO

begin new (Y);

Y^.VAL:=A;

if X^.VAL>A then

begin Y^.REF:=X; X:=Y end

else

begin

Z:=X;

U:=Z;

T:=true;

while (Z<>nil) and T do

begin T:=Z^.VAL<A;

U:=Z;

Z:=Z^.REF

end;

Y^.REF:=Z;

U^.REF:=Y;

end;

read (A)

end

end;

begin {MAIN PROGRAM}

YS(X);

PS(X);

{ S1NR(X);

PS(X)}

end.

Дерево поиска (сортировки).

Пример. Пусть задан массив чисел: 2 6 4 3 7 –2 8 5, его дерево поиска выглядит так:

2

-2 6

4 7

3 5 8

Оно строится следующим образом:

Последовательно для каждого значения элемента массива двигаемся по дереву, начиная с корня, до точки роста, к которой привешиваем этот элемент. При этом двигаемся по левой ветви, если значение подвешиваемого элемента меньше значения помещенного в этом узле элемента и по правой в противном случае. На языке Паскаль этот алгоритм может реализован процедурой pd, приведенной ниже. В этой реализации мы считаем, что признаком конца массива, расположенного во входном потоке, является появление нулевого значения.

program dersort;

type ref=^yz; yz=record i:integer; l,r:ref end;

var x:ref;

procedure pd(var x:ref);

var z,y,y1:ref;

a: integer;

begin read(a);

if a<>0 then

begin new(x); x^.i:=a; x^.l:=nil; x^.r:=nil;read(a);

while a<>0 do

begin y:=x; new(z); z^.i:=a; z^.l:=nil; z^.r:=nil;

while y<>nil do

begin y1:=y;

if a<y^.i then y:=y^.l else y:=y^.r

end;

if a<y1^.i then y1^.l:=z else y1^.r:=z;

read(a)

end

end

end;

procedure cod(var x:ref);

begin if x<>nil then

begin cod(x^.l); write(x^.i:3); cod(x^.r) end

end;

begin pd(x);cod(x) end.

Построенное дерево обладает следующим интересным свойством:

При симметричном обходе дерева поиска элементы массива перечисляются в порядке возрастания значений элементов.

Это свойство дерева поиска может быть положено в основу построения алгоритма сортировки элементов массива. Однако более интересной является обобщение этой задачи, которую можно сформулировать так:

Необходимость сортировки массив связано, в основном, с тем, что поиск конкретных значений элементов в упорядоченном массиве может быть осуществлен в среднем за O(log₂n), где n – число элементов в массиве, а в неупорядоченном за O(n). Предположим, что мы отказываемся от сортировки массивов, заменяя ее построением дерева поиска и поиском конкретных значений элементов в построенном дереве. Давайте оценим эффективность подобной замены.

Ограничимся рассмотрением случая, когда все элементы массива различны. Рассмотрим различные перестановки элементов массива и для каждой такой перестановки построим соответствующее ей дерево поиска. Оценим необходимое число сравнений различных элементов массива для поиска конкретного значения элемента в дереве поиска в среднем по всем возможным перестановкам элементов массива и среднее число сравнений для построения каждого такого дерева.

Пусть Т_n –мультимножество всех деревьев, соответствующее всем перестановкам элементов массива.

Замечание. Совокупность T_n действительно представляет мультимножество, однако, если узлы дерева помечать номерами мест откуда взято конкретное значение элемента массива то эта совокупность будет множеством.

Пример, n=3, элементы массива: 1 2 3, тогда возможны следующие деревья поиска:

1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1

1 1 2 2 3 3

2 3 1 3 1 3 1 2

3 2 2 1

1 1 1 1 1 1

2 2 2 3 3 2 2 2

3 3 3 3

Обозначим общее число вершин i-го уровня во всей совокупности T_n через m(i,n), а число точек роста, расположенных на i-том уровне, через q(i,n). Установим некоторые соотношение между m(i,n) и q(i,n).

Каждая вершина i-го уровня, при i>1, расположена в конце дуги, исходящей из вершины (i-1)-го уровня, а таких дуг равно удвоенному числу вершин (i-1)-го уровня за вычитом числа точек роста того же уровня, так что

m(i,n)=2 m(i-1,n) - q(i-1,n), i>1

Естественно принять, что m(i,n)=0, при i>n.

Рассмотрим теперь, что происходит при переходе от совокупности T_n к совокупности T_n+1. Каждое дерево из T_n порождает n+1 дерево совокупности T_n+1 соответственно его n+1 точке роста. В каждом из этих деревьев на уровне i сохраняются все вершины i-го уровня исходного дерева и, кроме того, в этой частичной совокупности из n+1 дерева к ним добавится столько новых вершин i-го уровня, сколько точек роста в исходном дереве на i-1, т.е.

m(i,n+1)=(n+1) m(i,n)+q(i-1,n), i>1.

Складывая, полученные равенства, получаем

m(i,n+1)=n m(i-1,n)+2m(i-1,n), i>1.

Число вершин первого уровня а совокупности T_n равно числу деревьев:

m(1,n)=n!

Оценим, теперь вычислительную сложность поиска конкретного значения элемента в дереве поиска. Прежде всего заметим, что если элемент находится в дереве на i-м уровне, то он обнаруживается после i сравнений.

Пусть tÎ T_n, t – конкретное дерево, обозначим для t число вершин i-го уровня через m^t(i), i=1,…,n. тогда среднее число сравнений необходимое для поиска в дереве t будет равно

k^t= .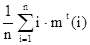

Но, нас интересует среднее значение числа сравнений по всем n! деревьям n-го порядка, образующих совокупность T_n. Оно равно

K(n) = = = .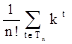

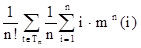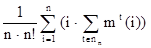Но, по определению, 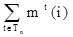= m(i,n), поэтому

k(n) = .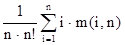

Опираясь на рекуррентное соотношение для m(i,n), можно получить аналогичное соотношение для k(n)

k(n) = ,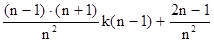

а с его помощью доказать (по индукции) справедливость выражения

k(n) = 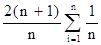-3, n³1.

Но 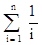= ln (n + O(1),

т.е. k(n) = 2 ln(n) + O(1) = 2^.ln(2)^.log₂(n) + O(1).

Так как 2^.ln(2)»1.39, среднее время поиска конкретного значения элемента в дереве поиска превышает минимально необходимое на 40%.

Перейдем к задаче определение средней сложности построения дерева поиска.

Пусть некоторому массиву соответствует дерево t, то элемент, размещающийся в вершине уровня i, займет свое место после i-1 сравнения. Отсюда число сравнений, затрачиваемых на организацию этого массива, равно

p^t = 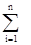(i-1)^.m^t(i) = 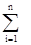i^.m^t(i) - 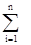^.m^t(i).

Первая сумма в этом выражении равна n^.k^t, а вторая дает n – число вершин дерева t, так что

p^t =n^.k^t-n.

Усредняя по всем деревьям из T_n, получаем выражение для среднего числа p(t) сравнений, требуемых для построения дерева:

P(t) = 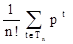= = 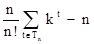n^.k(n)-n.

Используя выражение для k(n), получаем

p(n) = 2(n+1) 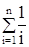- 4n.

Для больших n справедлива асимптотическая формула

p(n) = 2 n ln(n) + O(n) = 2^.n^.ln(2)^.log₂(n) + O(n).

Так что и здесь вычислительная сложность оказывается больше минимально необходимой в тоже число раз, что для поиска конкретного значения элемента в дереве поиска.

Упражнение. Определить дисперсию числа сравнений, необходимых для поиска конкретного значения элемента в дереве поиска. Эта дисперсия определяется выражением

d(n) = 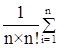(i-k(n))² m(i,n)

Деревья.

Определение. Связный граф без циклов называется деревом. Связный граф без циклов с выделенной вершиной называется корневым деревом. Выделенную вершину называют корнемдерева.

Легко определяются понятия: потомка, сына, предка, отца для данной вершины; понятие листа и внутренней вершины.

В программировании большой интерес представляют деревья, вершины которого помечены метками, отличающие одну вершину от другой. В дальнейшем будем считать, что в дереве с n вершинами в качестве меток используются числа 1,…,n.

Заметим, что одно и тоже непомеченное дерево может быть помечено различными способами, т. е. двум различным помеченным деревьям может соответствовать одно и тоже непомеченное дерево.

Пример, n=3.

1 2 3 2 1 3

Теорема(Кэли,1897). Число помеченных деревьев с n вершинами равно n^n-2.

Доказательство (Прюфер,1917).

Пусть дерево с n вершинами, помеченными числами 1, …,n. Свяжем с этим деревом последовательность натуральных чисел i₁,…,i_n-2 , построенную следующим образом:

1)положим j=0;

2)повторим следующий процесс n-2 раза:

увеличим значение j на единицу; найдем в дереве лист, помеченный натуральным числом с наименьшим значением. Пусть это значение k_j, и пусть отцом листа k_j является вершина, помеченная числом i_j. Выберем значение i_j в качестве j-ого элемента последовательности. Удалим в дереве ребро (i_j,k_j).

После исполнения этого алгоритма начальное дерево преобразуется в дерево, состоящее из одного ребра либо (i_n-2,n), либо, в случае i_n-2=n, – из ребра (n,n-1).