ТЕМА 4. ГЕНЕРАЦИЯ K-ПОДМНОЖЕСТВ
Подмножество, содержащее к элементов заданного множества А из n элементов (k£n), обычно называют K-подмножествами просто K-множествами. Для представления K-подмножеств, наряду с представлением в виде n-последовательностей нулей и единиц, которое обычно применяют только для хранения в упакованном виде, часто используется представление в виде K-кортежей натуральных чисел. При этом каждый кортеж считается упорядоченным, например, в порядке возрастания. Это связано с тем, что чаще k£n/2. (Так как K-множество и его дополнение однозначно связаны, и поставленную перед пользователем задачу удается переформулировать, используя либо K-множество, либо его дополнение.) Поэтому при хранении K-множеств в виде n-последовательностей нулей и единиц не менее половины из них являются нулями. При хранении K-кортежами могут, например, указываться порядковые номера элементов, входящих в K-множество.
Пример. Множеству (0,0,0,0,1,1,0,1,1,0,0) соответствует кортеж (5,6,8,9).
Перейдем теперь к алгоритму генерирования K-подмножеств в лексикографическом порядке. Прежде всего дадим определение лексикографической упорядоченности в терминах K-кортежей.
Определение. Множество (а1,...,аk), a1<...<ak, предшествует множеству (b1,...,bk), b1<...<bk, если существует i, 1£i£k, такое, что для любого j, j<i, aj=bj, ai<bi.
Упражнение. Доказать, что это определение эквивалентно определению лексикографической упорядоченности из п.3.1.
Первым в лексикографическом порядке является кортеж (1,...,k), а последним - (n-k+1,...,n). Пусть (а1,...,аk) не совпадает с последним кортежем генерации, тогда непосредственно следующим за ним является (b1,...,bk) = (а1,...,ap-1,ap+1,ap+2,...,ap+k-p+1), где р=max(i : ai<n-k+i). При этом, если (b1,...,bk) не последний, то следующий за ним выглядит так: (b1,...,br-1,br+1,br+2,...,br+k-r+1), где r=p-1, если bk=n, и k, если bk<n.
Пример. Генерации K- подмножеств в лексикографическом порядке. n=5, k=2.
1.(1,2) 5.(2,3) 8.(3,4) 10.(4,5)
p=2 p=2 p=2
2.(1,3) 6.(2,4) 9.(3,5)
p=2 p=2 p=1
3.(1,4) 7.(2,5)
p=2 p=1
4.(1,5)
p=1
Это приводит к следующему алгоритму на языке Паскаль:
program SUBSET1;
const n= ; k= ; (k<=n)
var s : array[1..k] of 1..n;
i,p : integer;
begin
for i:=1 to k do
{1} s[i]:=i; {задание первого K-множества}
p:=k;
while p>=1 do
begin
for i:=1 to k do write(s[i]); writeln;
{вывод очередного K-множества}
if s[k]=n then p:=p-1 else p:=k;
if p>=1 then
begin
s[p]:=s[p]+1;
for i:=p+1 to k do
{3} s[i]:=s[i-1]+1
end
end
end.
Оценим вычислительную сложность программы. Заметим, что оператор сроки {1} исполняется k раз; строки {2} - C 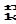 раз; а строки {3} - C
раз; а строки {3} - C 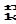 -1+ C
-1+ C 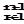 -1+....+ C
-1+....+ C 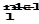 -1 раз, равное C
-1 раз, равное C 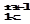 -k-1. То есть вычислительная сложность программы O(C
-k-1. То есть вычислительная сложность программы O(C 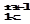 ). Учитывая, что C
). Учитывая, что C 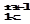 = C
= C 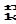 ×[(n+1)/(n-k+1)] и C
×[(n+1)/(n-k+1)] и C 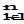 ×[k/(n-k+1)], получаем, что алгоритм линеен, за исключением случаев, когда k=n-o(n). В этом случае алгоритм можно применить для порождения (n-k)-подмножеств, с последующим переходом к их дополнению.
×[k/(n-k+1)], получаем, что алгоритм линеен, за исключением случаев, когда k=n-o(n). В этом случае алгоритм можно применить для порождения (n-k)-подмножеств, с последующим переходом к их дополнению.
Упражнение. Написать вариант программы SUBSET1 для K-подмножеств, представленных n-последовательностями нулей и единиц. Оценить вычислительную сложность построенной программы.
4.1Генерация K-подмножеств заменой одного элемента.
Для того чтобы убедиться в том, что подобные генерации существуют, рассмотрим некоторые свойства симметрично-отраженных кодов Грея.
Обозначение. Пусть a-некоторая цепочка над алфавитом Х. Тогда am, где m - целое неотрицательное число, обозначает конкатенацию m раз цепочки a.
Пример. Х={a,b,c} (ab)3=ababab ab3=abbb.
В дальнейшем симметрично-отраженный код Грея n-го порядка, генерируемый программой SET2, будем обозначать G(n). Естественно, что любое кодовое слово из G(n) является цепочкой длины n над {0,1}. Последовательности кодовых слов из G(n), содержащие k единиц и упорядоченные соответственно с их генерацией программой SET2, будем обозначать G(n,k). Последовательности, в которых кодовые слова располагаются в обратном порядке по отношению к G(n) или G(n,k), будем обозначать GR(n) и GR(n,k) соответственно.
Теорема 4.1. Первым кодовым словом в G(n) ровно k единицами будет 1k0n-k, а последним - 1k-10n-k1 и 0n, если k=0.
Доказательство проводится индукцией по n, при n=1 - очевидно. Пусть теорема справедлива для i£n и любых k, покажем, что теорема справедлива для n+1 и всех k. В терминах G(n) соотношение {1} из п.3.2 может быть записано как G(n+1)=G(n)0;GR(n)1, поэтому первое кодовое слово с k³0 единицами (кроме k=n+1) есть первое кодовое слово в G(n) с приписанным справа нулем. Иными словами, 1k0n+1-k, как и требовалось. Аналогично последнее кодовое слово с k³1 единицами в G(n) c приписанной справа единицей - это 1k-10n-k+11, как и требовалось. В случае k=n+1 единственным словом в G(n+1), содержащим n+1 единицу, является 1n+1.
Теорема 4.2. Соседние кодовые слова в G(n,k) различаются ровно в двух разрядах.
Доказательство проводится индукцией по n. Теорема, очевидно, справедлива для n=1, поскольку k=0, либо k=1. Предположим, что теорема верна для n и всех k, 0£k£n. Покажем, что она верна для n+1 и любого k, 0£k£n+1. Если k=0 или k=n+1, она справедлива, так как G(n+1) содержит только одно соответствующее кодовое слово. Для 1£k£n теорема выполняется по индукционному предположению, если кодовые слова оба либо в G(n)0 либо GR(n)1. Таким образом, требуется только рассмотреть, на сколько разрядов отличается последнее кодовое слово с k единицами в G(n)0 от первого кодового слова с k единицами в GR(n)1. Из предыдущей теоремы следует, что эти слова имеют вид: при k=1 0n-110 и 0n1, при k>1 1k-210n-k10 и 1k-200n-k11 соответственно.
Следствие. Последовательность кодовых слов G(n,k), n³k³0, можно определить следующей рекурсией:
G(n,k)=G(n-1,k); GR(n-1,k-1)1 и G(n,0)=0n, G(n,n)=1n. {2}
В самом деле, это определение действительно задает последовательность, совпадающую с той, которая получается удалением из G(n) всех кодовых слов с числом единиц, не равным k.
Рекурсивное определение {2} приводит к следующей программе генерации кодовых слов G(n,k) на языке Паскаль.
program subset2;
const n= ; k= ; {0<k<=n}
var i : integer;
s:array[1..n] of 0..1;
procedure print (m,h:integer);
begin
if h<>0 then h:=1;
for i:=1 to m do s[i]:=h;
for i:=1 to n do write(s[i]);
Дата добавления: 2015-08-11; просмотров: 807;
