Program subset3;

const n= ; k= ; n1= ; n2= ; {n1=n+1, n2=n+2}

var i,m,h:integer;

s:array[1..n1] of 0..1; {генерируемое кодовое слово}

t:array[1..n1] of 1..n2; { стек узлов}

Begin

for i:=1 to k do

begin s[i]:=1; t[i]:=i+1 end;

for i:=k+1 to n1 do

begin s[i]:=0; t[i]:=i+1 end;

h:=k;

t[1]:=k+1; {t[1] указывает на вершину стека}

m:=0;

while m<>n1 do

Begin

for i:=1 to n do write(s[i]); writeln;

{вывод очередного кодового слова}

m:=t[1];

t[1]:=t[m];

t[m]:=m+1; {выбор сына узла ветвления}

if s[m]=1 then

begin if h<>0 then s[h]:=1-s[h]

else s[m-1]:=1-s[m-1];

h:=h+1

End

Else

begin if h<>1 then s[h-1]:=1-s[h-1]

else s[m-1]:=1-s[m-1];

h:=h-1

End;

s[m]:=1-s[m]; {конец корректировки кодового слова}

if(h=m-1)or(h=0) then h:=h+1

Else begin

h:=h-s[m-1]; {корректировка h}

{1} t[m-1]:=t[1];

if h=0 then t[1]:=m-1

{2} else t[1]:=h+1

{корректировка стека}

End

End

End.

Комментарий. Стек реализуется таким же способом, как в SET4 t[1] указывает на узел в вершине стека, и каждый элемент t[j] в стеке немедленно получает новое значение, как только он исключается из стека. Присваивания {1} и {2} служат для добавления в стек m-1,...,h+1.

Упражнения. 1. Доказать корректность программы SUBSET3.

2. Откорректировать программу так, чтобы она правильно функционировала при k=0.

Литература

1. Ю. В. Матисевич. Десятая проблема Гильберта. М.: Физматлит, 1993

2. В. Липский. Комбинаторика для программистов. Мир, М. 1988.

3. Х Минк. Перманенты. Мир, М. 1982.

4. Э. Рейнгольд, Ю. Нивергельт, Н. Део. Комбинаторные алгоритмы. Теория и практика. Мир. М. 1980.

Процедурные типы.

В Turbo Pascal процедуры и функции можно рассматривать как некоторые параметры и можно использовать переменные, принимающие значение процедуры или функции. С этой целью вводятся процедурные типы, которые указывают, какой вид подпрограммы (процедуру или функцию) можно использовать в качестве параметра и с какими параметрами должны быть эти подпрограммы.

Объявление процедурного типа похоже на заголовок подпрограммы: пишется слово procedure или function, за которым в круглых скобках записывается список формальных параметров; для функции после списка формальных параметров через двоеточие указывается тип функции. В отличие от заголовка подпрограммы здесь не указывается имя подпрограммы.

Пример.

type

proc1=procedure; {процедура без параметров}

proc2=procedure (var x,y:integer);

{процедура с двумя параметрами-переменными типа integer}

func1=function (x:real):real;

{функция типа real с одним параметром типа real}

Далее можно ввести переменные этих типов:

var

p1 : proc1;

p2 : proc2;

f1 : func1;

После этого процедурным переменным можно присваивать значения конкретных процедур и функций. Как и в во всех других случаях, процедурная переменная и подпрограмма должны быть совместимы для присваивания.

Существует ряд правил использования подпрограмм в качестве процедурной переменной:

- они должны компилироваться с ключом компилятора {$F+} или иметь директиву far для получения полного адреса подпрограмм;

- они не должны быть стандартными процедурами и функциями;

-они не должны объявляться внутри других процедур и функций;

- они не должны быть типа inline или interrupt.

Пример.

{$f+}

procedure swap(var a,b:integer);

var t: integer;

begin t:= a; a:= b; b:= t end;

function tan( angle: real): real

begin tan:= sin(angle)/ cos( angle)

{проверка, что cos( angle)<>0, осуществляется в самой программе}

end;

{$f-}

в этом случае процедурным переменным, введенным ранее, можно присвоить значения:

p2:=swap;

f1:= tan;

а вызовы p2(i,j) и f1(x) эквивалентны соответственно swap(i,j) и tan(x).

Так же как и указатель, процедурная переменная занимает 4 байта памяти, в которых помещается полный адрес подпрограммы (поэтому подпрограммы необходимо компилировать с ключом {$f-}.

Процедурные переменные можно использовать так же, как и переменные других типов: в выражениях ( если эта переменная – функция), в виде оператора ( если эта переменная – процедура), как компонента другой более сложной переменной, как передаваемый в подпрограмму параметр. Идея единства данных и подпрограмм получила дальнейшее развитие в объектно-ориентированном программировании.

Пример. Вычисление интеграла по формуле Симпсона.

Для аппроксимации интеграла

s=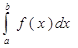

используется сумма конечного числа узловых значений f_i.

s_k= 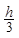(f₀+4f₁+2f₂+4f₃+2f₄+. . .+4f_n-3+2f_n-2+4f_n-1+f_n)

где f_i=f(a+i_*h), h=(b-a)/n и n=2^k. Число узловых точек равно n+1, а h – расстояние между двумя соседними узловыми точками. Значение интеграла s аппроксимируется последовательностью s₁, s₂,…, которая сходится, если функция ведет себя достаточно хорошо (гладкая) и если арифметические операции выполняются точно.

На каждом шаге число узловых точек удваивается. Конечно, хорошая программа не будет вычислять f(x) 2^k раз на каждом k-м шаге, поскольку можно использовать значения f_i, полученные на предыдущих шагах. В сумме s_k три члена

s_k= s 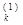+ s + s

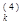
которые обозначают суммы в узловых точках с весами 1, 2, 4. Их можно определить с помощью рекуррентных соотношений для к>1:

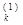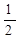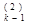
s = 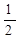s

s 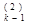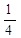= s + s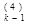

s 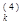= 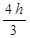(f(a+h)+f(a+3h)+…+f(a+(n-1)h))

и начальных значений:

s = 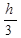(f(a)+f(b))

s 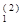=0

s =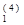

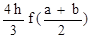
program integral;

const pi=3.141592;

type func1=function (x:real):real;

var ep:real;

{$f+}

function bil(x:real):real;

var a1,a2:real; i:integer;

begin a1:=sin(10*x); a2:=sin(x);if a2=0 then a1:=1 else a1:=a1/a2;

bil:=a1*a1*a1*a1*a1*a1;

end;

function bi(x:real):real;

begin bi:=sin(x) end;

{$f-}

function simpson(a,b:real; f:func1):real;

var i,n:integer;

s,ss,s1,s2,s4,h:real;

begin n:=2;h:=(b-a)*0.5;

s1:=h*(f(a)+f(b)); s2:=0;

s4:=4*h*f(a+h); s:=s1+s2+s4;

repeat ss:=s; n:=2*n; h:=h/2;

s1:=0.5*s1; s2:=0.5*s2+0.25*s4;

s4:=0; i:=1;

repeat s4:=s4+f(a+i*h); i:=i+2

until i>n;

s4:=4*h*s4; s:=s1+s2+s4

until abs(s-ss)<ep;

simpson:=s/3

end{simpson};

begin ep:=0.001;writeln((1/(2*pi))*simpson(0,2*pi,bil));

writeln(simpson(0,pi/2,bi))

end.