Полуэмпирические модели шума струй

Затопленная струя

Основу полуэмпирической модели шума затопленной реактивной струя составляют рассмотренные выше полуэмпирические графо-аналитические соотношения, определяющие мощность, направленность и спектр акустического излучения струи.

1/ Мощность акустического излучения определяется с помощью выражении (5.18), полученного с помощью метода размерностей на основе акустической аналогии Лайтхилла:

,

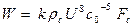где: F_с – площадь поперечного сечения сопла в плоскости среза, U_с – скорость истечения реактивной струи, к – коэффициент пропорциональности, величина которого получена экспериментально и при значении плотности 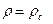равна:

к = 0.8 10 ^-4 – для газовых струй, истекающих из дозвукового сопла,

к = 1.5 10 ^-4 – для реактивных струй ТРД при работе на взлетном и номинальном режимах,

к = 2.5 10 ^-4 – для реактивных струй ТРД при работе двигателя на режимах ниже номинального.

2/ Суммарный по спектру излучения уровень звукового давления (L_c) определяется по известным мощности излучения (W) и фактору направленности (10lgФ) на основе соотношения (5.19):

,

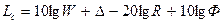, (5.22)

где 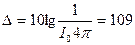дБ – для случая излучения в сферу, и дБ – для случая излучения в полусферу. Фактор направленности акустического излучения (10lgФ) определяется с помощью обобщенной графической зависимости, приведенной на рисунке 5.14.

3/ Спектр звукового давления в третьоктавных полосах частот рассчитывается на основе обобщенных спектров звукового давления (рисунок 5.16) в соответствии с соотношением:

, (5.23)

где 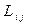- спектральный уровень звукового давления в третьоктавной полосе с центральной частотой f_i в направлении θ_j , L_сj – суммарный уровень звукового давления для направления распространения звука “θ_j” , 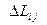- ординаты обобщенных спектров звукового давления затопленной струи (рисунок 5.16) для частот излучения, определенных для соответствующих чисел критерия подобия – числа Струхаля .

Соотношения (5.18, 5.22, 5.23) справедливы для дозвуковых изотермических и неизотермических струй, температура торможения ко­торых не превышает 10ОО°К, а перепад давления на срезе сопла - не более 2.5.

Струя в спутном потоке

Закономерности генерации шума струей, распространяющейся в спут­ном потоке воздуха, обычно используются на практике для оценки влия­ния скорости полета самолета на интенсивность шума реактивной струи ТРД или ТРДД и в методике расчета шума реактивной струи ТРДД. От дос­товерности этих закономерностей зависит надежность методики расчета шума на местности самолетов, у которых доминирующим источником шума является реактивная струя.

Известен ряд методов оценки влияния спутного потока на интенсив­ность шума, излучаемого реактивной струей. Методы отличаются структурой расчетных соотношений. Так расчет уровня звуковой мощности струи в путном потоке производится в соответствии с зависимостями:

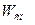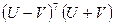~ (5.24)

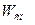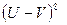~ (5.25)

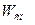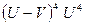~ (5.26)

где U- скорость истечения реактивной струи, V - скорость спутного потока или скорость полета.

Экспериментальные исследования шума струи в спутном потоке пока­зали. что параметр (U-V) не адекватно отражает влияние спутного потока на интенсивность акустического излучения струи (рисунок 5.19). Шум затопленной струи, скорость истечения которой равна (И-V), c ростом величины " V " уменьшается значительно быстрее, нежели шум струи с постоянной скоростью истечения "U”, но распространяющейся в спутном потоке, скорость которого равна "V".

Известно, что при постоянной скорости истечения струи увеличение скорости спутного потока вплоть до значения параметра спутности 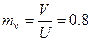практически не изменяет наклона профиля средней скорости вблизи се­редины зоны смешения; то есть величина максимального поперечного градиента продольной составляющей скорости потока слабо зависит от скорости спутного потока и, следовательно, от разности скоростей (U-V).

Снижение шума струи под влиянием спутного потока происхо­дит в первую очередь за счет уменьшения градиента средней скорости в той области зоны смешения струи, которая непосредственно примыкает к спутному потоку. Градиент скорости в этой области пропорционален разности скоростей на ее границах , а так как 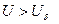, то 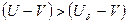. Поэтому и влияние спутного потока на шум будет слабее, чел это следует , если использовать в оценках разность скоростей (U-V).

Ранее было показано, что акустическая мощность струи, расп­ространяющейся в спутном потоке, зависит от величины параметра спутности ( 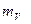} и начальной турбулентности спутного потока (рисунок 5.19). Пос­кольку до настоящего времени практически нет данных о микроструктуре неизотермических реактивных струй, то для инженерных расчетов можно использовать следующее соотношение:

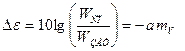(5.27)

где m_v =1.95 - эмпирическая константа, полученная на основе резуль­татов экспериментального исследования шума изотермических струй. Соотношение при m_v =1.95 согласуется с эксперименталь­ными данными по влиянию скорости полета на шум реактивной струи ТРД.

Обобщенные характеристики направленности и спектр акустического излучения изотермической струи в спутном потоке совпадают с соответ­ствующими характеристиками затопленной струи. Нагрев затопленной струи приводит к изменению лишь характеристики направленности, а обобщен­ный спектр шума остается практически без изменения .

Анализ результатов летных испытаний самолетов с ТРДД с низкой степенью духконтурности показывает, что для неизотермической реактивной струи, распространяющейся в движущейся среде - атмосфере, имеют место ана­логичные явления. Таким образом, для расчета акустических характеристик неизотермической реактивной струи ГТД, распространяющейся в спутном потоке, получены следующие соотношения:

мощность акустического излучения:

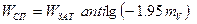(5.28)

суммарный уровень звукового давления

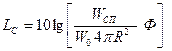(5.29)

где фактор напрвленности " Ф - аппроксимация соответствующих экспериментальных обобщенных зависимостей.

Уровень звукового давления в i-й третьоктавной полосе частот равен:

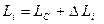(5.30)

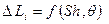, (5.31)

где - критерий Струхаля.

Соотношения (5.28-5.31) справедливы для дозвуковых изотермических и неизотермических струй, температура торможения ко­торых не превышает 10ОО°К, а перепад давления на срезе сопла - не более 2.5.

Соосные струи

В настоящее время известны различные методы расчета акустической мощности соосных струй. В некоторых методах рассматривается три основных источника шума: в начальном участке - это области смешения внутреннего и периферийного потока между собой и с окружающей средой, а в переходном и основном уча­стках - зона смешения условной осесимметричной струи, истекающей из сопла экви­валентного (при одинаковом импульсе с соосными струями) диаметра.

Акустическая мощность начального участка внешней струи и основного участка эквивалентной струи рассчитывается как для обычной затопленной струи, а акустическая мощность начального участка внутренней струи определяется как для струи в спутном потоке, то есть:

,

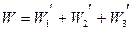где 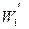- акустическая мощность внешней струи в пределах на­чального участка, 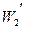- акустическая мощность внутренней струи в пределах начального участка, 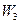^’ - акустическая мощность ос­новного участка струи эквивалентного диаметра.

При достаточно больших размерах внешней струи расчетная схема может быть упрощена, так как в этом случае отпадает необходимость в учете мощности акустического излучения струи эквивалентного диаметра. Это обстоятельство позволяет предложить более про­стую схему расчета, при которой общая акустическая мощность соосных струй представляет собой сумму мощностей акустического излучения внешней и внутренней струй. При этом периферийный поток рассматривается как затопленная струя, а внутренний поток— как струя, истекающая в спутный поток ограниченных поперечных размеров.

Соотношение для расчета акустической мощности в этом случае может быть представлено в следующем виде:

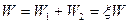_1зат + W₂ , (5.32)

где W₁ - акустическая мощность внутреннего потока в системе соосных струй, W_1зат - акустическая мощность внутреннего потока при отсутствии внешней струи, W₂ - акустическая мощность пе­риферийного потока, 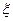- корректирующая функция. Расчет вели­чин W_1зат и W₂ проводится по известным формулам для обычной затопленной струи. Для определения значения функции 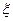может быть использовано эмпирическое соотношение, полученное для изотермических струй:

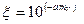(5.33)

где 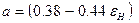, 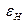- интенсивность начальной турбулент­ности спутного потока, которая изменяется в интервале от 0,5 до 12%.

На основании соотношения (5.32) выражение для уровня акусти­ческой мощности изотермических соосных струй может быть запи­сано в следующем виде:

, (5.34)

или

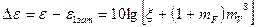(5.35)

где 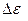- избыточный уровень акустической мощности соосных струй относительно акустической мощности струи внутреннего контура, распространяющейся в невозмущенной среде. Результаты расчета уровней звукового давления изотермической соосной струи, вы­полненного на основе соотношения (5.34), хорошо согласуются с экспериментальными данными (рисунок 5.22) , полученными для струи с параметрами m_F = 2,87 и m_V = 0.25 - 1.0 во всем диапа­зоне изменения параметра спутности.

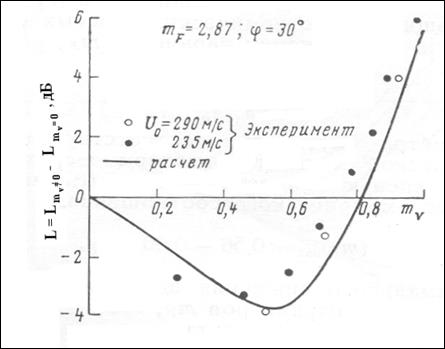
Рисунок 5.22

В экспериментах получено, что акустическая мощность неизотер­мических струй изменяется пропорционально третьей степени от­ношения термодинамических температур струи вне зоны смеше­ния 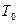и окружающей среды 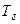, то есть

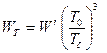, (5.36)

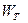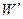где и — акустические мощности неизотермической и изо­термической струй. Тогда на основе соотношений (5.33), (5.34) и (5.36) при­ближенное выражение для мощности акустического излучения неизотермических соосных струй можно записать в следующем виде:

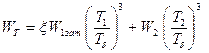. (5.37)

Соответственно для избыточного уровня акустической мощности расчетное соотношение имеет вид:

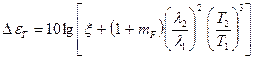. (5.38)

Результаты расчета уровня акустической мощности реактивной струи ТРДД со степенью двухконтурности 2 и парамет­рами струи: m_F = 0.51, T₂ / T₁ = 0,43 - 0,46 и = 1, выполненного в соответствии с соотношением (5.37) для различных режимов работы двигателя, с точностью до 2 дБ совпадают с данными, полученными на основе измерений шума реактивной струи двигателя в стендо­вых условиях.

Изложенная методика расчета акустической мощности изо­термических и неизотермических соосных струй позволяет провести анализ влияния соотношений газодинамических и геометрических параметров потоков на срезе сопел на уровень суммарной акусти­ческой мощности струй. Ниже представлены результаты такого анализа, выполненного для двух различных условий: сохранения постоянства избыточного импульса внутренней струи и сохране­ния равенства тяг соосных струй и некоторой фиктивной затоп­ленной струи.

Из соотношений (5.35) и (5.38) следует, что акустическая мощность изотермических соосных струй имеет наи­меньшее значение при значении параметра m_F ,равном (рисунок 5.23):

(5.39)

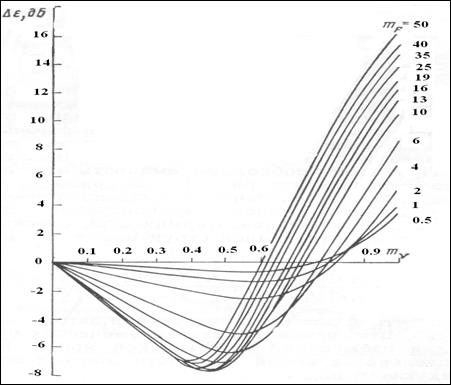
Рисунок 5.23

Значение параметра спутности, соответствующее наименьшему уровню акустической мощности изотермических соосных струй, с достаточной степенью точности может быть определено с помо­щью следующего соотношения:

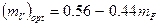. (5.40)

Величина максимального снижения шума неизотермических соос­ных струй зависит от параметров m_F , 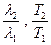(рисунок 5.24), причем увеличение m_F и 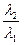приводит к снижению шума струй, а увели­чение отношения 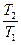- к возрастанию шума. Имеется оптимальное значение отношения 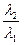, при котором наблюдается наиболь­шее снижение шума струи.

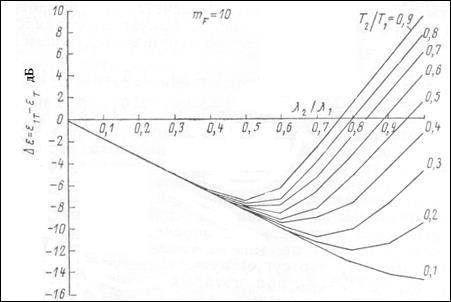
Рисунок 5.24

Для m_F ≤ 6 и 0.25 < 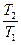< 1 соот­ветствующее эмпирическое соотношение имеет вид:

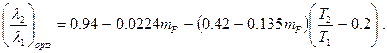(5.41)

Возвращаясь к выражению (5.21) для степени двухконтурности газотурбинного двигателя и принимая во внимание соотношения (5.33) и (5.34), определяющие оптимальные значения параметров m_F и 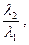можно отметить, что выбор наивыгоднейшей с точки зрения сни­жения шума реактивной струи степени двухконтурности двигателя зависит, в конечном счете, от выбора отношения температур по­токов .

При этом необходимо выбирать отношение темпера­тур возможно меньшим (рисунок 5.24), что приводит к уменьшению шума соосных струй, увеличению оптимального значения парамет­ров 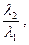и к увеличению степени двухконтурности двигателя.