Вектор Умова-Пойнтинга. Излучение диполя
Первые опыты с электромагнитными волнами в радиодиапазоне были осуществлены Г. Герцем в 1888 г. С помощью изобретенного им вибратора Герц получил направленные плоские волны длиной от 0,6 до 10 м. Он установил, что скорость распространения этих волн близка к скорости световых волн, а также доказал их поперечность. В 1896 г. А.С. Попов впервые передал на расстояние (~250 м) сообщение с помощью электромагнитных волн. Это были слова: "Генрих Герц". Тем самым было положено начало радиотехнике.
Энергия электромагнитных волн. Ранее были получены выражения для плотности энергии электрического (134) и магнитного полей по отдельности (151). Когда оба поля существуют одновременно, плотность энергии такого электромагнитного поля равна сумме энергий электрической и магнитной составляющих
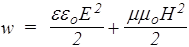 . (169)
. (169)
Поскольку в электромагнитной волне фазы Е и Н совпадают, следовательно, для любых значений Е и Н, взятых в один момент времени, ee0Е2=mm0Н2. Значит, плотности энергий электрической и магнитной составляющих одинаковы
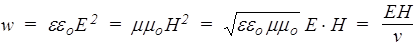 , (170)
, (170)
где v - скорость волны. Покажем, что v - это также скорость распространения электромагнитной энергии.
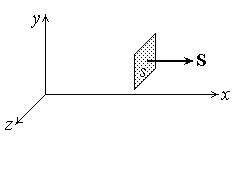
Введем вектор S, направленный вдоль скорости v, величина которого определяет энергию, переносимую волной в единицу времени через единичную площадку s, перпендикулярную v (рис.51),
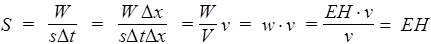 .
.
|
Мы умножили числитель и знаменатель дроби на Dх, чтобы выделить w. Последнее верно и в векторной форме (так как векторы Е, Н и v - взаимно перпендикулярны и образуют правовинтовую систему)
S = [E´H]. (171)
| Рис.51 |
Вектор S называется вектором Умова-Пойнтинга и представляет собой плотность потока электромагнитной энергии
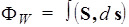 . (172)
. (172)
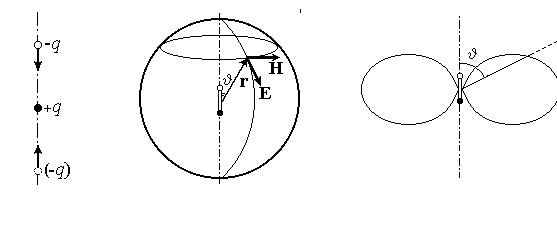
Излучение диполя. Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь (рис.52).
Свяжем систему отсчета с положительным зарядом диполя, тогда положение отрицательного заряда будет определяться радиус-вектором r. Пусть дипольный момент этой системы изменяется по закону
p= -qr = -qlercos wt = pm cos wt,
где l - амплитуда колебаний (длина диполя); er - единичный вектор вдоль r; pm=-qler.
|
| Рис.52 |
| Рис.54 |
| Рис.53 |
Рассмотрим излучение малого по сравнению с длиной волны диполя(l<<l) на расстоянии r>>l . Расчет показывает, что если такая волна распространяется в однородной изотропной среде, то ее фронт будет сферическим (рис.53), а амплитуда по мере роста r постепенно убывает. При этом v (и S) совпадает с направлениемr, а Е и Н перпендикулярны v, образуя правовинтовую систему. В каждой точке векторы Е и Н колеблются по закону cos(wt-kr). Амплитуды Еm и Нm зависят от угла J и убывают обратно пропорционально r
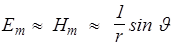 . (173)
. (173)
Среднее значение плотности потока энергии <S>~ЕmНm, поэтому
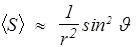 . (174)
. (174)
Максимальную энергию диполь излучает в направлении, перпендикулярном своей оси (J =p/2), а вдоль оси (J = 0; p) - не излучает вообще.
Расчет показывает, что мощность излучения диполя N пропорциональна квадрату второй производной дипольного момента по времени
N ~ ( 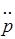 )2 =
)2 = 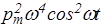 .
.
Усредняя по времени, получаем среднюю мощность
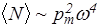 . (175)
. (175)
Таким образом, средняя мощность излучения диполя пропорциональна квадрату амплитуды дипольного момента и четвертой степени частоты. Например, для частоты переменного тока 50 Гц, считая, что амплитуда дипольного момента имеет порядок величины pm~10-27 Кл×м (как у типичных полярных молекул), получим, что один грамм вещества излучает ~10-25Вт! Обычно такие потери для линий электропередач можно считать незначительными по сравнению с тепловыми потерями.
Так как р=-qr (по определению дипольного момента), то
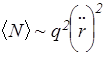 . (176)
. (176)
Таким образом, средняя мощность излучения пропорциональна квадрату ускорения заряженной частицы. Расчеты показывают, что это верно не только для колебательного, но и для любого движения зарядов, а именно: всякий заряд, движущийся с ускорением, излучает электромагнитные волны, причем мощность этого излучения пропорциональна квадрату его ускорения.
Например, электроны, ускоренные в бетатроне (см. лекцию 8), излучают электромагнитные волны за счет центростремительного ускорения 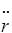 =v2/R, теряя при этом мощность ~v4. Поэтому возможное ускорение электронов ограничено пределом ~500 МэВ , когда потери на излучение становятся равными энергии, сообщаемой электронам вихревым электрическим полем.
=v2/R, теряя при этом мощность ~v4. Поэтому возможное ускорение электронов ограничено пределом ~500 МэВ , когда потери на излучение становятся равными энергии, сообщаемой электронам вихревым электрическим полем.
В соответствии с выражением (176), заряд, движущийся без ускорения, не излучает энергии. В частности, электрон, движущийся с постоянной скоростью, не излучает электромагнитных волн. Однако в 1934 г. С.А. Вавиловым и П. А.Черенковым было обнаружено, что это правило нарушается для электрона, движущегося со скоростью, большей скорости света в данной среде  .
.

|
| Рис.55 |
|
| Рис.56 |
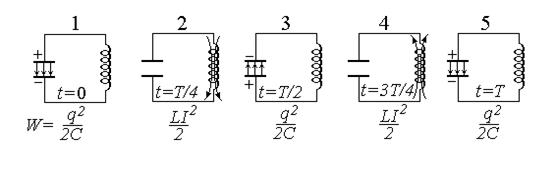
Электрические колебания. Заряд, совершающий гармонические колебания, излучает монохроматическую волну с частотой, равной частоте колебаний заряда. Электрические колебания могут возникать в колебательном контуре – цепи, содержащей индуктивность и емкость (рис.55). Если повернуть ключ K в положение 1, то конденсатор зарядится до напряжения, равного величине эдс источника. Замкнем ключ в положение 2. В начальный момент (t=0) вся энергия будет сосредоточена в электрическом поле конденсатора (ситуация 1 на рис.56). Конденсатор начнет разряжаться, через катушку L потечет ток, и электрическая энергия конденсатора начнет преобразовываться в энергию магнитного поля катушки. Когда конденсатор полностью разрядится (рис.56,2), ток в цепи достигнет максимума. Затем ток начнет убывать, не меняя направления, причем постепенно, так как его будет поддерживать эдс самоиндукции. Этот ток будет перезаряжать конденсатор, возникнет электрическое поле противоположного направления по сравнению с начальным, так как теперь положительно будет заряжена нижняя пластина. Это поле будет стремиться ослабить ток, который прекратится в момент, когда заряд на конденсаторе достигнет максимума (Рис.56,3). После этого конденсатор опять начнет разряжаться, ток потечет в обратном направлении (Рис.56,4), после чего возникнет состояние, идентичное исходному (Рис.56,5). Далее процесс будет повторяться. Так возникают периодические колебания (заряда на обкладках конденсатора, напряжения на конденсаторе и тока через катушку).
|
| Рис.57 |
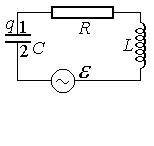
Найдем дифференциальное уравнение колебаний в контуре, содержащем емкость С, индуктивность L, активное сопротивление R и источник переменной эдс e (рис.57). Будем считать положительным направление обхода контура по часовой стрелке. Пусть q - заряд верхней обкладки (тогда знаки тока и заряда совпадают). В соответствии с законом Ома для участка цепи 1®R®L®2
RI = j1 - j2 + es + e,
где es - эдс самоиндукции es=-L×dI/dt=-L×d2q/dt2; j2-j1=q/C (так как для q>0 должно быть j2>j1). Следовательно,
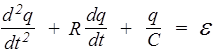 . (177)
. (177)
Это неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Ему можно придать канонический вид
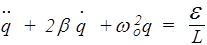 , (178)
, (178)
если ввести обозначения 2b = R/L, w 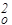 = 1/LC. Здесь имеется полная аналогия с механическими затухающими колебаниями, где w0 - собственная частота, b - коэффициент затухания. Если e=0, то такие колебания называются свободными.
= 1/LC. Здесь имеется полная аналогия с механическими затухающими колебаниями, где w0 - собственная частота, b - коэффициент затухания. Если e=0, то такие колебания называются свободными.
Свободные незатухающие колебания. Это - частный случай уравнения (178) при e=0 и R=0
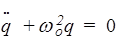 . (179)
. (179)
Решение этого уравнения рассматривалось в механике
q = qm cos(wot + a). (180)
Величины qm и a определяются начальными условиями. Поскольку wо=(LC)-1, собственная частота определяется только свойствами контура. Отсюда легко получить выражение для То (То=2p/wо) - собственного периода колебаний, называемое формулой Томпсона
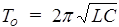 . (181)
. (181)
Дифференцируя выражение (180) по времени, можно найти ток
I = dq/dt = -qm wosin(wot + a). (182)
Так как функция sin сдвинута относительно cos на p/2, ток в контуре опережает заряд по фазе на p/2 (и напряжение U=q/C, которое меняется в одной фазе с зарядом на конденсаторе).
Свободные затухающие колебания. Реальный контур всегда обладает некоторым активным сопротивлением, которое нагревается при прохождении тока. Переход части электромагнитной энергии в тепловую необратим, поэтому энергия колебаний будет уменьшаться со временем. Положив в (178) e=0, получим однородное дифференциальное уравнение
 . (183)
. (183)
Нетрудно убедиться, что решение этого уравнения (при b2<wо2) имеет вид:
q = qm e-bt cos(wt + a), (184)
где 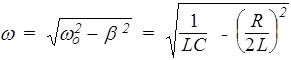 . Функция (184) не является периодической. Но можно рассматривать ее как "периодическую" с периодом Т:
. Функция (184) не является периодической. Но можно рассматривать ее как "периодическую" с периодом Т:
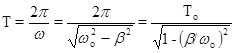 (185)
(185)
|
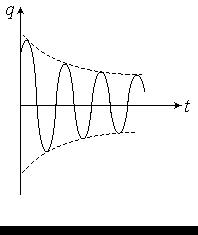
и амплитудой qme-bt, экспоненциально уменьшающейся со временем (рис.58). Зная q(t), можно найти напряжение на конденсаторе и ток в контуре
 ,
,
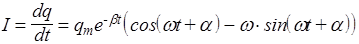 .
.
| Рис.58 |
Последнее выражение с использованием тригонометрических формул нетрудно преобразовать к виду
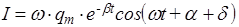 ,
,
где sind=w/wo, причем p/2<d<p. А это значит, что при наличии активного сопротивления R ток в контуре опережает по фазе напряжение более, чем на p/2!
Вынужденные электрические колебания. Пусть в контур см. (рис.57) включена внешняя переменная эдс
 .
.
Тогда уравнение (178) будет выглядеть следующим образом:
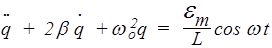 . (186)
. (186)
Решение этого неоднородного уравнения представляет собой сумму общего решения однородного уравнения (т.е. с правой частью, равной нулю) и частного решения неоднородного. Общее решение (184) однородного уравнения является затухающим. Следовательно, по прошествии достаточного времени установившиеся колебания будут следовать частному решению
q = qm cos(wt - g), (187)
что легко проверить, подставляя его в уравнение (186). Однако технически удобнее сначала найти I(t), а затем q(t). Дифференцируя (187), получаем: I=Imcos(wt-j), где j - сдвиг фаз между током и внешней эдс (e), Im=wqm, j=g-p/2. Тогда
UR = RI = RIm×cos(wt-j),
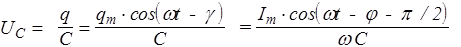 ,
,
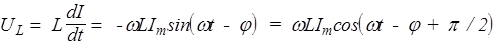 .
.
|
| Рис.59 |
| Рис.60 |
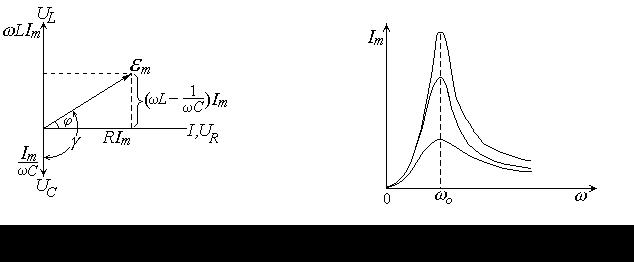
Из последней формулы видно, что фазы величин UR и I совпадают. UC отстает от I на p/2, a UL - опережает I на p/2. Наглядно это можно изобразить при помощи векторной диаграммы (рис.59), из которой ясно, что em представляет собой векторную сумму всех слагаемых (UR, UC и UL). Следовательно,
 .
.
 .
.
Как видно из полученных выражений, амплитуда тока максимальна, когда wL-1/wC=0, и резонансная частота равна
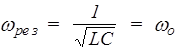 . (188)
. (188)
Таким образом, резонансная частота wрез для силы тока совпадает с собственной частотой колебательного контура wo. На рис. 60 представлены резонансные кривые для тока в зависимости от w. Чем меньше b=R/2L, тем острее резонанс. Вследствие сдвига фаз резонансные кривые для q, UC, UL не достигают максимума при wо.
Дата добавления: 2015-08-14; просмотров: 3696;
