Лекция 19. Распространение света в анизотропных средах. Интерференция поляризованного света
|
| Рис.69 Рис.70 |
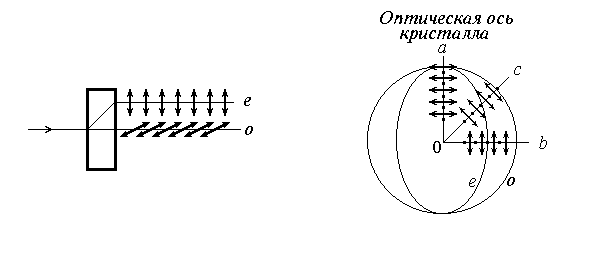
При падении света на поверхность многих кристаллов наблюдается явление двойного лучепреломления: внутри кристалла луч разделяется на два, имеющие различные скорости и направления. У одноосных кристаллов (так называются кристаллы, у которых существует направление, называемое оптической осью, вдоль которого не происходит разделения на два луча) один из преломленных лучей - обыкновенный (о) - подчиняется обычным законам преломления, другой - необыкновенный (е) - не подчиняется. В частности, необыкновенный луч не лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. Установлено, что оба луча (о и е) полностью поляризованы в двух взаимно перпендикулярных направлениях (рис.69). Плоскость колебаний обыкновенного луча перпендикулярна главному сечению кристалла (так называется любая плоскость, проходящая через оптическую ось), а необыкновенного - совпадает с ним. Двойное лучепреломление объясняется анизотропией кристаллов, диэлектрическая проницаемость которых зависит от направления, изменяясь от e|| до e^; e|| и e^ - диэлектрическая проницаемость кристалла в параллельном оптической оси направлении и в перпендикулярном соответственно. Так как n2=e и n=с/v, следовательно, в этих направлениях будут различаться и скорости распространения света. Таким образом, волнам с различными по отношению к оптической оси направлениями колебаний вектора Е соответствует различная скорость распространения.
Рассмотрим три из возможных направлений распространения обыкновенного луча - a, b и с (рис.70) в одноосном кристалле. В каждом из них вектор Е направлен перпендикулярно оптической оси кристалла (точки), поэтому скорости распространения будут одинаковы 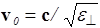 . Изображая величину скорости отрезками, отложенными по разным направлениям, можно получить сферу (круг в сечении плоскостью чертежа). Эта сфера является волновой поверхностью обыкновенных лучей для источника, расположенного в точке 0. Для тех же трех направлений в необыкновенном луче вектор Е (стрелки) образует разные углы a c оптической осью: p/2 - для луча а (его скорость
. Изображая величину скорости отрезками, отложенными по разным направлениям, можно получить сферу (круг в сечении плоскостью чертежа). Эта сфера является волновой поверхностью обыкновенных лучей для источника, расположенного в точке 0. Для тех же трех направлений в необыкновенном луче вектор Е (стрелки) образует разные углы a c оптической осью: p/2 - для луча а (его скорость 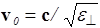 ); a=0 для луча b (его скорость
); a=0 для луча b (его скорость 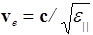 ). Для луча с скорость имеет промежуточное значение. Можно доказать, что волновая поверхность необыкновенных лучей представляет собой эллипсоид.
). Для луча с скорость имеет промежуточное значение. Можно доказать, что волновая поверхность необыкновенных лучей представляет собой эллипсоид.
Таким образом, одноосные кристаллы характеризуются двумя показателями преломления: n0=c/v0 и ne=c/ve. В зависимости от того, какая из скоростей больше, различают положительные (ve<v0) и отрицательные (ve>v0) одноосные кристаллы.
Интерференция поляризованных лучей. При наложении двух когерентных, но поляризованных во взаимно перпендикулярных направлениях лучей интерференционной картины получиться не может. Интерференция возникает только тогда, когда складываются однонаправленные колебания.
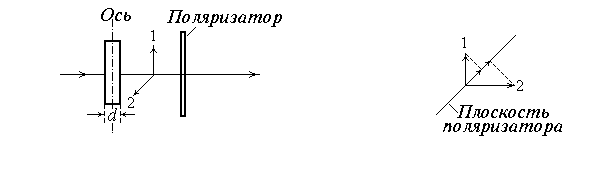
Рассмотрим наложение обыкновенного и необыкновенного лучей, вышедших из кристаллической пластинки, вырезанной параллельно оптической оси (рис.71а). При падении луча перпендикулярно к пластинке обыкновенный и необыкновенный лучи пойдут не разделяясь, но с различными скоростями. На выходе из пластинки между ними возникнет разность хода
D = (no - ne) d (203)
и разность фаз
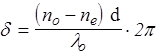 , (204)
, (204)
|
| Рис.71 |
| а |
| б |
где d - толщина пластинки, l0 - длина волны в вакууме. При этом выходящие лучи будут поляризованы во взаимно перпендикулярных плоскостях. Поставим на пути этих лучей поляризатор, после прохождения которого колебания обоих лучей будут лежать в одной плоскости (рис.71,б). Однако они все равно не будут интерферировать. Дело в том, что естественный свет представляет собой множество беспорядочно сменяющих друг друга цугов волн, испускаемых отдельными атомами. Обыкновенный луч происходит из цугов с близкими направлениями плоскостей колебаний, а необыкновенный - из цугов с перпендикулярными этому направлению плоскостями. Поскольку отдельные цуги некогерентны, то и лучи должны быть некогерентны.
Если на пластинку падает плоскополяризованный свет, то колебания каждого цуга раскладываются между обыкновенным и необыкновенным лучами в определенной пропорции, зависящей от ориентации оптической оси пластинки и плоскости колебаний в падающем луче. Возникая из одного цуга, соответствующие доли в обыкновенном и необыкновенном лучах оказываются когерентными и будут интерферировать.
Вырезанная параллельно оптической оси пластинка, для которой
D = (no - ne) d = mlo + lo/4,
называется пластинкой в четверть волны. Если D = (no - ne)d=mlo+lo/2, то такая пластинка называется пластинкой в полволны. При прохождении пластинки в четверть волны обыкновенный и необыкновенный лучи приобретают разность фаз p/2, в полволны - p.

|
| Рис.72 Рис.73 |
Рассмотрим прохождение света через пластинку в полволны. Колебание вектора Е при входе в кристалл разделится на колебания Еo и Еe - обыкновенного и необыкновенного лучей соответственно (рис.72). За время прохождения пластинки разность фаз между колебаниями Е0 и Еe изменится на p. Поэтому свет, поляризованный на входе в плоскости Р, на выходе будет поляризован в плоскости Р'. Плоскости Р и Р' расположены симметрично относительно оптической оси пластины О. Таким образом, пластинка в полволны поворачивает плоскость колебаний на угол 2j, где j - угол между плоскостью колебаний в падающем луче и осью пластинки.
Пропустим плоскополяризованный свет через пластинку в четверть волны (рис.73). Если плоскость колебаний в падающем луче составляет угол 45° с осью пластинки, амплитуды обоих лучей на выходе будут одинаковы. Сдвиг фаз составит p/2. Следовательно, вышедший свет будет поляризован по кругу. При ином значении угла j амплитуды вышедших лучей будут разными, поэтому при наложении колебаний эти лучи дадут свет, поляризованный по эллипсу, одна из осей которого совпадает с осью пластинки.
При пропускании плоскополяризованного света через пластинку другой толщины из нее выйдут две когерентные, поляризованные во взаимно перпендикулярных плоскостях волны, разность фаз которых отличается от p/2 и p. Поэтому на выходе получится эллиптически поляризованный свет, причем ни одна из осей эллипса не будет совпадать с осью пластинки.
Если на пути эллиптически поляризованного света поставить пластинку в четверть длины волны, расположив ее оптической осью вдоль одной из осей эллипса, то пластинка внесет дополнительную разность фаз, равную p/2. В результате разность фаз двух плоскополяризованных волн, дающих в сумме эллиптически поляризованную волну, станет равной нулю или p, так что на выходе будет получена плоскополяризованная волна. Следовательно, надлежащим образом повернутая пластинка в четверть волны превращает эллиптически поляризованный свет в плоско-поляризованный. Это позволяет различать виды поляризации света. Например, исследуемый свет пропускается через пластинку в четверть волны и затем через поляризатор. Если исследуемый свет является эллиптически поляризованным, то, вращая пластинку и поляризатор вокруг направления луча, удается добиться полного затемнения поля зрения. Если свет является только частично поляризованным или неполяризованным, то погашения достичь не удается ни при каком взаимном положении пластинки и поляризатора.
|
| Рис.74 |
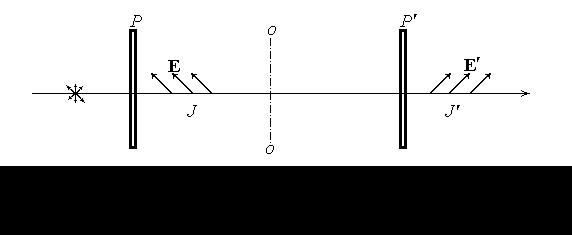
Кристаллическая пластинка между двумя поляризаторами. Поместим между поляризаторами Р и Р' пластинку из одноосного кристалла, вырезанную параллельно оптической оси О (рис.74) Из поляризатора Р выйдет плоскополяризованный свет интенсивности J. После прохождения пластинки свет станет в общем случае эллиптически поляризованным. После прохождения поляризатора Р' (его в этом случае называют анализатором), свет снова станет плоскополяризованным. Его интенсивность J' зависит от взаимной ориентации плоскостей поляризаторов и разности фаз, приобретаемой при прохождении пластинки.
Пусть угол j между плоскостью поляризатора Р и осью пластинки О равен p/4. Рассмотрим два частных случая: поляризаторы параллельны (рис.75) и скрещены (рис.76). После поляризатора Р вектор Е лежит в плоскости Р. При входе в пластинку вектор Е разложится на два когерентных колебания: Ео - перпендикулярное и Еe - параллельное оси. Амплитуды этих колебаний одинаковы и равны
Eo = Ee = E cos(p/4) = E/ 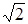 ,
,
где Е - амплитуда волны, вышедшей из первого поляризатора. Через второй поляризатор пройдут составляющие колебаний Е0 и Еe в направлении плоскости Р'. Амплитуды этих составляющих равны амплитудам Е0 и Еe, умноженным на cos(p/4), т.е.
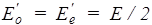 .
.
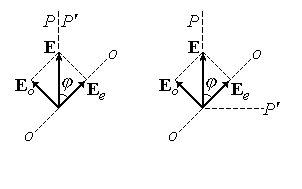
|
| Рис.75 Рис.76 |
Если поляризаторы параллельны, то разность фаз после поляризатора Р' равна d - разности фаз, приобретенной после прохождения пластинки. Если поляризаторы скрещены, то проекции векторов Е0 и Еe на направление Р' будут иметь разные знаки, следовательно, в дополнение к d возникает еще разность фаз, равная p. После второго поляризатора волны будут интерферировать. В случае параллельных поляризаторов амплитуда результирующей волны
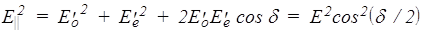 . (205)
. (205)
А в случае скрещенных -
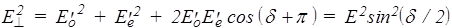 . (206)
. (206)
Интенсивность пропорциональна квадрату амплитуды, поэтому
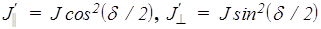 .
.
Здесь  и
и 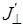 - интенсивности света после второго поляризатора для параллельного и перпендикулярного их взаимного расположения соответственно; J - интенсивность света после первого поляризатора. Нетрудно видеть, что
- интенсивности света после второго поляризатора для параллельного и перпендикулярного их взаимного расположения соответственно; J - интенсивность света после первого поляризатора. Нетрудно видеть, что
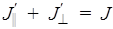 .
.
Таким образом, интенсивность распределяется без потерь.
Дата добавления: 2015-08-14; просмотров: 1818;
